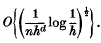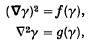Research Article
Classes of unipotent elements in simple algebraic groups. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-18
-
- Article
- Export citation
On characteristically simple groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-35
-
- Article
- Export citation
Finite distributive quasigroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-41
-
- Article
- Export citation
On group actions on groups and associated series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-55
-
- Article
- Export citation
Iterated torus knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-60
-
- Article
- Export citation
A wild automorphism of Usl(2)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-65
-
- Article
- Export citation
Associative h-spaces and algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-69
-
- Article
- Export citation
Syntopogenous preordered spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-79
-
- Article
- Export citation
A general theory of separation, regularity, and connectedness properties
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-90
-
- Article
- Export citation
Regularity of the Segre stratification
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-97
-
- Article
- Export citation
Geometric versions of Whitney regularity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-101
-
- Article
- Export citation
The Stone-Čech compactification of a topological semigroup
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-107
-
- Article
- Export citation
Maximal one-sided ideals in Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-111
-
- Article
- Export citation
Inclusion conditions for Hurwitzian and Schur sets in
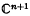
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-120
-
- Article
- Export citation
Discreteness of the singular spectrum for Schrödinger operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-133
-
- Article
- Export citation
On a Gaussian process related to multivariate probability density estimation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-144
-
- Article
- Export citation
Stochastic models with electrical analogues
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-151
-
- Article
- Export citation
Prototurbulent motions in dissipative model systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-163
-
- Article
- Export citation
Complex potential equations I. A technique for solution
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-187
-
- Article
- Export citation
On the elasticity of monatomic crystals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-211
-
- Article
- Export citation

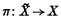 →
→ 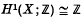 and let
and let 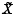 . Various authors (1), (2), have shown that, for iterated torus knots,
. Various authors (1), (2), have shown that, for iterated torus knots, 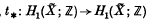 is of finite order (i.e. some power of
is of finite order (i.e. some power of 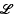 we define
we define 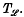 . The family of separation axioms so obtained is shown to include all the standard axioms
. The family of separation axioms so obtained is shown to include all the standard axioms 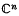 is a finite constructible stratification: in this paper we verify this statement, and show moreover that it is a Whitney stratification. Some of the arguments are by no means special to the case in hand; however, there seems little point in attempting a general formulation. It is a pleasure to acknowledge helpful conversations with Professor C. T. C. Wall and Dr E. J. N. Looijenga.
is a finite constructible stratification: in this paper we verify this statement, and show moreover that it is a Whitney stratification. Some of the arguments are by no means special to the case in hand; however, there seems little point in attempting a general formulation. It is a pleasure to acknowledge helpful conversations with Professor C. T. C. Wall and Dr E. J. N. Looijenga.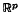 ,
, 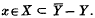 . In (4) C. T. C. Wall considered the following conditions:
. In (4) C. T. C. Wall considered the following conditions: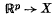 ,
, 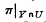 is a submersion.
is a submersion. satisfies (*) if every maximal one-sided ideal in
satisfies (*) if every maximal one-sided ideal in 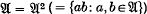 satisfy (*), and they mentioned a conjecture that if
satisfy (*), and they mentioned a conjecture that if 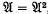 , then
, then 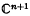
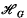 of
of 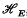 , where
, where 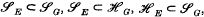 where
where  denotes the Schur set of
denotes the Schur set of