We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The complex variable method is applied to obtain solutions for the deflexion of a supported circular plate with uniform line loading along an eccentric circle under a general boundary condition including the clamped boundary 
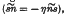, a boundary with zero peripheral couple 
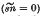, a boundary with equal boundary cross-couples 
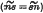, a hinged boundary 
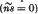and a boundary for which 
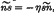, η being Poisson's ratio. These solutions are used to obtain the deflexion at any point of a circular plate having an eccentric circular patch symmetrically loaded with respect to its centre. Expressions for the slope and cross-couples over the boundary and the deflexions at the centres of the plate and the loaded patch are obtained.