Research Article
Fibonacci and Lucas polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-387
-
- Article
- Export citation
On generic hypersurfaces in ℝn
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-394
-
- Article
- Export citation
Normal bundles in flag bundles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 395-402
-
- Article
- Export citation
An independence theorem for automorphisms of torsion-free groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 403-409
-
- Article
- Export citation
Groups whose irreducible representations have finite degree
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 411-421
-
- Article
- Export citation
On Banach modules I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 423-444
-
- Article
- Export citation
Representation theory for tensor products of Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 445-463
-
- Article
- Export citation
Characters and contact transformations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 465-476
-
- Article
- Export citation
The structure of type I JBW-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-482
-
- Article
- Export citation
Codimension one immersions and the Kervaire invariant one problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-493
-
- Article
- Export citation
The factorization of simple knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 495-506
-
- Article
- Export citation
Conserved currents of the Klein–Gordon field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 507-515
-
- Article
- Export citation
Conditions for an affine manifold with torsion to have a Riemann–Cartan structure*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 517-527
-
- Article
- Export citation
Spindle-shaped drops in a viscous extensional flow
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 529-536
-
- Article
- Export citation
The Variational Principle and natural transformations I. Autonomous dynamical systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 537-560
-
- Article
- Export citation
Proceedings of meetings
Proceedings of the meetings held during the session 1980-1981
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 561-567
-
- Article
- Export citation
Front matter
PSP volume 90 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 90 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b14
-
- Article
-
- You have access
- Export citation

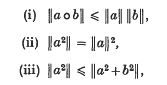
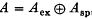
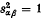 ). By theorems 15 and 16 of (11) any type
). By theorems 15 and 16 of (11) any type