Let G be a finite group, Sn be the symmetric group on n symbols and An be the corresponding alternating group. The conjugacy classes of the wreath product G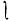 Sn (or monomial group as it is sometimes known) and the conjugacy classes of G
Sn (or monomial group as it is sometimes known) and the conjugacy classes of G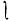 An have been described by Kerber (see [2] and [3]). The group Sn has a double cover
An have been described by Kerber (see [2] and [3]). The group Sn has a double cover 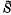 n so that the faithful complex representations of this double cover may be regarded as protective representations of Sn. In Section 2, a particular double cover for G
n so that the faithful complex representations of this double cover may be regarded as protective representations of Sn. In Section 2, a particular double cover for G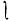 Sn is constructed, the faithful complex representations of this group being the subject of a joint article with Peter Hoffman[1]. In the present paper, our task is to determine whether a conjugacy class of G
Sn is constructed, the faithful complex representations of this group being the subject of a joint article with Peter Hoffman[1]. In the present paper, our task is to determine whether a conjugacy class of G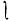 Sn corresponds to one or to two conjugacy classes in the double cover of G
Sn corresponds to one or to two conjugacy classes in the double cover of G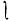 Sn (and similarly for G
Sn (and similarly for G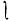 An). The main results, Theorems 1 and 2, are stated precisely in Section 2 and proved in Sections 3 and 4 respectively. The case when G = 1 provides classical results of Schur ([5], Satz IV). When G is a cyclic group, Read [4] has determined the conjugacy classes, not just for our particular double cover, but for all possible double covers of G
An). The main results, Theorems 1 and 2, are stated precisely in Section 2 and proved in Sections 3 and 4 respectively. The case when G = 1 provides classical results of Schur ([5], Satz IV). When G is a cyclic group, Read [4] has determined the conjugacy classes, not just for our particular double cover, but for all possible double covers of G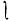 Sn.
Sn.