Research Article
A quadratic recurrence of Faltung type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-197
-
- Article
- Export citation
On projective planes of type (6, m)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-204
-
- Article
- Export citation
Tripos theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-232
-
- Article
- Export citation
One-relator quotients of free products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-243
-
- Article
- Export citation
The decomposition of crystal families
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 245-263
-
- Article
- Export citation
Canonical stratifications of functions: the simple singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-272
-
- Article
- Export citation
On real simple singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-279
-
- Article
- Export citation
On the equations defining tangent cones
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-297
-
- Article
- Export citation
A convex 3-complex not simplicially isomorphic to a strictly convex complex
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-306
-
- Article
- Export citation
Collapsing three-dimensional convex polyhedra: correction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-310
-
- Article
- Export citation
Resolving acyclic images of three-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 311-319
-
- Article
- Export citation
A note on 3-fold branched coverings of S3
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-325
-
- Article
- Export citation
The distance to upper triangular operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-329
-
- Article
- Export citation
Subspaces with property (b) in locally convex spaces of quasi-barrelled type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-337
-
- Article
- Export citation
On the Williams-Bjerknes tumour growth model: II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 339-357
-
- Article
- Export citation
Basic stress analysis of hyperbolic regimes in plastic media
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 359-369
-
- Article
- Export citation
Overall properties of a cracked solid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 371-384
-
- Article
- Export citation
Front matter
PSP volume 88 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 88 issue 2 Cover, Back matter and Corrigendum
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation

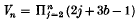 and
and 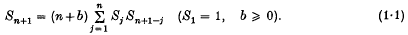


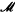 ) be a local ring,
) be a local ring, 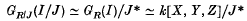
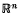 is called
is called 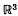 having the property that at least one vertex of the triangulation lies in the interior of a face of
having the property that at least one vertex of the triangulation lies in the interior of a face of