Research Article
Classification of crystal lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-349
-
- Article
- Export citation
A note on orthogonality and permutability of subnormal subgroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-355
-
- Article
- Export citation
Infinitely divisible projective representations of the Lie algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-368
-
- Article
- Export citation
Codimension and analytic spread
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-373
-
- Article
- Export citation
Uniqueness of an independent transversal of a family of sets†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-380
-
- Article
- Export citation
Cayley maps and symmetrical maps
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-386
-
- Article
- Export citation
Sur l'ensemble des points fixes des actions de S1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-392
-
- Article
- Export citation
Multipliers on some sequence spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-401
-
- Article
- Export citation
Harmonic analysis of scalar and vector fields in
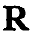 n
n
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 403-416
-
- Article
- Export citation
Inclusion relations for Riesz typical means
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-423
-
- Article
- Export citation
Difference-covers that are not k-sum-covers. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-438
-
- Article
- Export citation
On hearing the shape of a drum: an extension to higher dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 439-447
-
- Article
- Export citation
A bivariate Poisson queueing process that is not infinitely divisible
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 449-450
-
- Article
- Export citation
The calculation of diagonal matrix elements of two-body relative state operators between many-body oscillator states
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-456
-
- Article
- Export citation
The calculation of matrix elements of three particle operators in α-particle nuclei
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 457-458
-
- Article
- Export citation
A decomposition identity for a class of Riemannian invariants†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-463
-
- Article
- Export citation
The instability of a vortex sheet on a subsonic stream under acoustic radiation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 465-488
-
- Article
- Export citation
An existence theorem for Robin's equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-498
-
- Article
- Export citation
An axisymmetric contact problem: the constriction of elastic cylinders under axial compression
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 499-514
-
- Article
- Export citation
Proceedings of Meetings
Proceedings of the meetings held during the session 1971–72
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 515-519
-
- Article
- Export citation

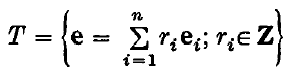
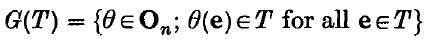
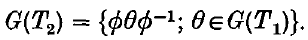


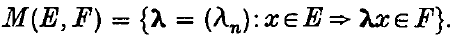

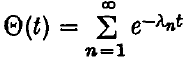 may be constructed in identical fashion; thus
may be constructed in identical fashion; thus