Research Article
On ideals of finite homoloǵical dimension in local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 941-948
-
- Article
- Export citation
A note on the homology of ideals ǵenerated by three elements in local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 949-952
-
- Article
- Export citation
On the complexes of Hirsch and Eilenberǵ–Moore
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 953-960
-
- Article
- Export citation
A proof of Newman's theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 961-963
-
- Article
- Export citation
Separation axioms for topological ordered spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 965-973
-
- Article
- Export citation
On the invariance of the essential spectrum of an arbitrary operator. III
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 975-984
-
- Article
- Export citation
The inductive limit of uncountably many compact Abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 985-987
-
- Article
- Export citation
Minimal decompositions in partially ordered normed vector spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 989-1000
-
- Article
- Export citation
On product sets in a unimodular group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1001-1007
-
- Article
- Export citation
Linear operators with closed range
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1009-1010
-
- Article
- Export citation
Properties of certain measures on a topological group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1011-1013
-
- Article
- Export citation
Large families of singular measures having absolutely continuous convolution squares
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1015-1022
-
- Article
- Export citation
Generalization of Hölder's and Minkowski's inequalities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1023-1027
-
- Article
- Export citation
On Nörlund summability of derived Fourier series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1029-1031
-
- Article
- Export citation
Definite integrals involving Whittaker functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1033-1039
-
- Article
- Export citation
An integral involving the G-function and Kampé de Fériet function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1041-1044
-
- Article
- Export citation
Certain recurrence relations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1045-1048
-
- Article
- Export citation
Use of Gauss' hypergeometric function and Meijer's G-function in the production of heat in a cylinder
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1049-1054
-
- Article
- Export citation
A note on the asymptotic expansion of the second Appell function
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 1055
-
- Article
- Export citation
On a recent theorem of Carleson. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1057-1059
-
- Article
- Export citation

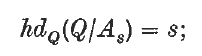
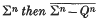
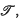 , <) is a set
, <) is a set 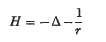
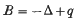
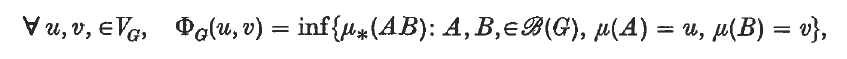
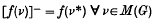
 (
(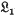 -algebra has large dimension. This answers a question (6.4) left open in (3).
-algebra has large dimension. This answers a question (6.4) left open in (3).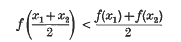
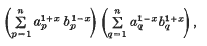
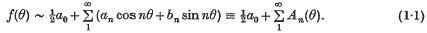
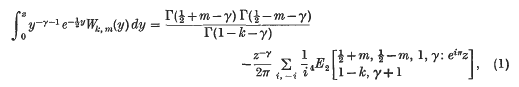
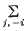 means that in the expression following it
means that in the expression following it