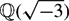Let 0 ⩽ α ⩽ ∞ and ψ be a positive function defined on (0, ∞). In this paper, we will study the level sets L(α, {ψ(n)}), B(α, {ψ(n)}) and T(α, {ψ(n)}) which are related respectively to the sequence of the largest digits among the first n partial quotients {Ln(x)}n≥1, the increasing sequence of the largest partial quotients {Bn(x)}n⩾1 and the sequence of successive occurrences of the largest partial quotients {Tn(x)}n⩾1 in the continued fraction expansion of x ∈ [0,1) ∩ ℚc. Under suitable assumptions of the function ψ, we will prove that the sets L(α, {ψ(n)}), B(α, {ψ(n)}) and T(α, {ψ(n)}) are all of full Hausdorff dimensions for any 0 ⩽ α ⩽ ∞. These results complement some limit theorems given by J. Galambos [4] and D. Barbolosi and C. Faivre [1].

The Delaunay tessellation of a locally finite subset of the hyperbolic space ℍn is constructed via convex hulls in ℝn+1. For finite and lattice-invariant sets it is proven to be a polyhedral decomposition, and versions (necessarily modified from the Euclidean setting) of the empty circumspheres condition and geometric duality with the Voronoi tessellation are proved. Some pathological examples of infinite, non lattice-invariant sets are exhibited.

We study the expected number of real zeros for random linear combinations of orthogonal polynomials. It is well known that Kac polynomials, spanned by monomials with i.i.d. Gaussian coefficients, have only (2/π + o(1))logn expected real zeros in terms of the degree n. If the basis is given by the orthonormal polynomials associated with a compactly supported Borel measure on the real line, or associated with a Freud weight defined on the whole real line, then random linear combinations have expected real zeros. We prove that the same asymptotic relation holds for all random orthogonal polynomials on the real line associated with a large class of weights, and give local results on the expected number of real zeros. We also show that the counting measures of properly scaled zeros of these random polynomials converge weakly to either the Ullman distribution or the arcsine distribution.

We study infinite families of quadratic and cubic twists of the elliptic curve E = X0(27). For the family of quadratic twists, we establish a lower bound for the 2-adic valuation of the algebraic part of the value of the complex L-series at s=1, and, for the family of cubic twists, we establish a lower bound for the 3-adic valuation of the algebraic part of the same L-value. We show that our lower bounds are precisely those predicted by the celebrated conjecture of Birch and Swinnerton-Dyer.

We show how the theory of linear forms in two logarithms allows one to get very good effective irrationality measures for nth roots of rational numbers a/b, when a is very close to b. We give a p-adic analogue of this result under the assumption that a is p-adically very close to b, that is, that a large power of p divides a−b. As an application, we solve completely certain families of Thue–Mahler equations. Our results illustrate, admittedly in a very special situation, the strength of the known estimates for linear forms in logarithms.

We investigate the operation of torus surgery on tori embedded in S4. Key questions include which 4–manifolds can be obtained in this way, and the uniqueness of such descriptions. As an application we construct embeddings of 3–manifolds into 4–manifolds by viewing Dehn surgery as a cross section of a surgery on a surface. In particular, we give new embeddings of homology spheres into S4.

A poset model of a topological space X is a poset P such that the subspace Max(P) of the Scott space ΣP is homeomorphic to X, where Max(P) is the set of all maximal points of P. Every T1 space has a (bounded complete algebraic) poset model. It was, however, not known whether every T1 space has a directed complete poset model and whether every sober T1 space has a directed complete poset model whose Scott topology is sober. In this paper we give a positive answer to each of these two problems. For each T1 space X, we shall construct a directed complete poset E that is a model of X, and prove that X is sober if and only if the Scott space Σ E is sober. One useful by-product is a method for constructing more directed complete posets whose Scott topology is not sober.

We provide a new and concise proof of the existence of suprema in the Cuntz semigroup using the open projection picture of the Cuntz semigroup initiated in [12]. Our argument is based on the observation that the supremum of a countable set of open projections in the bidual of a C*-algebra A is again open and corresponds to the generated hereditary C*-subalgebra of A.

A multi-crossing (or n-crossing) is a singular point in a projection of a knot or link at which n strands cross so that each strand bisects the crossing. We generalise the classic result of Kauffman, Murasugi and Thistlethwaite relating the span of the bracket polynomial to the double-crossing number of a link, span〈K〉 ⩽ 4c2, to the n-crossing number. We find the following lower bound on the n-crossing number in terms of the span of the bracket polynomial for any n ⩾ 3:

We unconditionally determine , the set of possible prime degrees of cyclic K-isogenies of elliptic curves with -rational j-invariants and without complex multiplication over number fields K of degree ≤ d, for d ≤ 7, and give an upper bound for for d > 7. Assuming Serre's uniformity conjecture, we determine exactly for all positive integers d.

We use twisted Alexander polynomials to show that certain algebraically slice 2-bridge knots are not topologically slice, even though all prime power Casson–Gordon signatures vanish. We also provide some computations indicating the efficacy of Casson–Gordon signatures in obstructing the smooth sliceness of 2-bridge knots.