Research Article
Etale homotopy and sums-of-squares formulas
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 1-25
-
- Article
- Export citation
Generalized Euler constants
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 27-41
-
- Article
- Export citation
Homotopy limits for 2-categories
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 43-63
-
- Article
- Export citation
Integrality and the Laurent phenomenon for Somos 4 and Somos 5 sequences
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 65-85
-
- Article
- Export citation
Upper bounds of Hilbert coefficients and Hilbert functions
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 87-94
-
- Article
- Export citation
Criteria for components of a function space to be homotopy equivalent
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 95-106
-
- Article
- Export citation
Weak*- continuous homomorphisms of Fourier–Stieltjes algebras
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 107-120
-
- Article
- Export citation
Cones arising from C*-subalgebras and complete positivity
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 121-127
-
- Article
- Export citation
Gauss paragraphs of classical links and a characterization of virtual link groups
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 129-140
-
- Article
- Export citation
Harmonic morphisms with one-dimensional fibres on conformally-flat Riemannian manifolds
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 141-151
-
- Article
- Export citation
A note on finite determinacy for corank 2 map germs from surfaces to 3-space
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 153-163
-
- Article
- Export citation
On filling families of finite subsets of the Cantor set
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 165-175
-
- Article
- Export citation
Asymptotic behavior of distribution of frequencies of digits
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 177-195
-
- Article
- Export citation
Pair correlations of the leVeque sequence on the polydisc
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 197-203
-
- Article
- Export citation
Packing-dimension profiles and fractional Brownian motion†
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 205-213
-
- Article
- Export citation
Dimension of some non-normal continued fraction sets
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 215-225
-
- Article
- Export citation
An entire function with a Baker domain and sparsely distributed singular values
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 227-241
-
- Article
- Export citation
Estimations of the remainder of spherical harmonic series
-
- Published online by Cambridge University Press:
- 01 July 2008, pp. 243-255
-
- Article
- Export citation


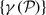 of generalized Euler constants arising from integers sieved by finite sets of primes
of generalized Euler constants arising from integers sieved by finite sets of primes 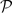 . For
. For  , the set of the first
, the set of the first  as
as 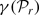 is monotonic in
is monotonic in 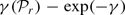 and the Riemann hypothesis.
and the Riemann hypothesis.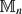 (
(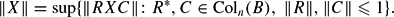
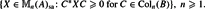
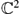 , 0) → (
, 0) → (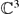 , 0). Examples and counter examples of such map germs are presented.
, 0). Examples and counter examples of such map germs are presented.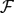 be a family of finite subsets of the Cantor set
be a family of finite subsets of the Cantor set  . Following D.H. Fremlin, we say that
. Following D.H. Fremlin, we say that 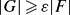 . We show that if
. We show that if 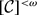 , then for every
, then for every 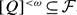 . A similar result for weaker versions of density is also obtained.
. A similar result for weaker versions of density is also obtained.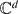 by
by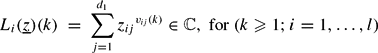
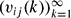 a strictly increasing sequence of natural numbers. Let
a strictly increasing sequence of natural numbers. Let 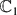 = {
= {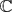 : |
: |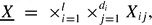 where for each pair (
where for each pair (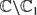 . We study the distribution of the sequence on the
. We study the distribution of the sequence on the 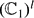 defined by the coordinatewise polar fractional parts of the sequence
defined by the coordinatewise polar fractional parts of the sequence 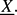 More precisely for arcs
More precisely for arcs 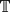 , let
, let 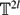 and for each
and for each 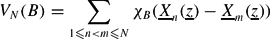
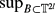 {
{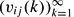 , that given ε > 0 we have Δ
, that given ε > 0 we have Δ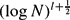 (log log
(log log 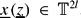 . Similar results on extremal discrepancy are also proved. Our results complement those of I. Berkes, W. Philipp, M. Pollicott, Z. Rudnick, P. Sarnak, R Tichy and the author in the real setting.
. Similar results on extremal discrepancy are also proved. Our results complement those of I. Berkes, W. Philipp, M. Pollicott, Z. Rudnick, P. Sarnak, R Tichy and the author in the real setting.