Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
M. Ram Murty
and
Anastasia Zaytseva
2013.
Transcendence of Generalized Euler Constants.
The American Mathematical Monthly,
Vol. 120,
Issue. 1,
p.
48.
Gun, Sanoli
Saha, Ekata
and
Sinha, Sneh Bala
2014.
Transcendence of generalized Euler–Lehmer constants.
Journal of Number Theory,
Vol. 145,
Issue. ,
p.
329.
Gun, Sanoli
Murty, V. Kumar
and
Saha, Ekata
2016.
Linear and algebraic independence of generalized Euler–Briggs constants.
Journal of Number Theory,
Vol. 166,
Issue. ,
p.
117.
Chatterjee, Tapas
and
Khurana, Suraj Singh
2019.
Shifted Euler constants and a generalization of Euler-Stieltjes constants.
Journal of Number Theory,
Vol. 204,
Issue. ,
p.
185.
Lichtman, Jared
and
Pomerance, Carl
2019.
The Erdős conjecture for primitive sets.
Proceedings of the American Mathematical Society, Series B,
Vol. 6,
Issue. 1,
p.
1.
Bharadwaj, Abhishek T
2020.
A short note on generalized Euler–Briggs constants.
International Journal of Number Theory,
Vol. 16,
Issue. 04,
p.
823.
Alkan, Emre
2020.
Biased behavior of weighted Mertens sums.
International Journal of Number Theory,
Vol. 16,
Issue. 03,
p.
547.
Alkan, Emre
2020.
Inequalities between sums over prime numbers in progressions.
Research in Number Theory,
Vol. 6,
Issue. 3,
Chatterjee, Tapas
and
Khurana, Suraj Singh
2022.
A series representation of Euler–Stieltjes constants and an identity of Ramanujan.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 1,
KANDHIL, NEELAM
and
LUNIA, RASHI
2024.
TRANSCENDENCE OF GENERALISED EULER–KRONECKER CONSTANTS.
Bulletin of the Australian Mathematical Society,
Vol. 109,
Issue. 3,
p.
464.


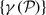 of generalized Euler constants arising from integers sieved by finite sets of primes
of generalized Euler constants arising from integers sieved by finite sets of primes 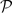 . For
. For  , the set of the first
, the set of the first  as
as 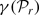 is monotonic in
is monotonic in 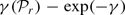 and the Riemann hypothesis.
and the Riemann hypothesis.