Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T02:54:07.056Z Has data issue: false hasContentIssue false
  • English
  • Français

A ‘Waring's problem’ for homogeneous forms

Published online by Cambridge University Press:  24 October 2008

W. J. Ellison
W. J. Ellison
Affiliation:
St Catharine's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Professor H. Davenport has raised the following question. Let f(X) be a homogeneous form in n variables X, of degree k, with coefficients in a field K. Is it possible to write f(X) in the form

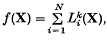
where the Li(X) are linear forms over K and N depends only on K, n, and k? In particular, what can be said when K = R, the reals; K = Q, the rationals; K = C, the complex numbers ?

We shall show that when k is odd such a representation is always possible and we shall obtain an explicit bound for N. However, if k is even, no such result is possible when K = R or Q, even when we impose the obvious necessary condition that f(X) be positive semi-definite. In fact we shall exhibit a construction for obtaining forms f(X) which are positive definite but cannot be expressed in the form

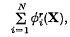
r even, where φi(X) is a homogeneous form of degree s and sr = k. We shall determine precisely which definite forms can be expressed in the required form. Some natural generalizations of the problem are then considered.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 3 , May 1969 , pp. 663 - 672
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hilbert, D.Über die Darstellung definiter Formen als Summe von Formen-quadraten. Math. Ann. 32 (1888), 342–350. (Ges. Abh. II, s. 154–161.)CrossRefGoogle Scholar
(2)Eggleston, H. G.Convexity. Cambridge Tracts in Mathematics and Mathematical Physics, no. 47.Google Scholar
(3)Elliot, E. B.Algebra of quantics (Oxford, 1895).Google Scholar
(4)Mordell, L. J. A new Waring problem with squares of linear forms. Quart. J. Math. (Oxford Ser.), 1 (1930), 276–288.Google Scholar
(5)Mordell, L. J.Representation of a binary cubic form as a sum of cubes. J. London Math. Soc. 11 (1936), 204–208.CrossRefGoogle Scholar
(6)Mordell, L. J.Binary cubic forms expressed as a sum of cubes. J. London Math. Soc. 42 (1967), 646–651.CrossRefGoogle Scholar
(7)Bourbaki, N.Eléments de Mathématique, VI. Intégration, Chapter III.Google Scholar