Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:40:45.492Z Has data issue: false hasContentIssue false
  • English
  • Français

The total Steenrod operation is induced by an A∞ ring homomorphism

Published online by Cambridge University Press:  24 October 2008

A. Kozlowski
A. Kozlowski
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI 48202, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a (based) space of the homotopy type of a CW-complex. Let H(X) denote the classical (ungraded) cohomology ring Πi≥0Hi (X;Z/2). In [1] Atiyah and Hirzebruch described the group 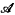of natural ring automorphisms of H(X) (‘cohomology automorphisms’) with group operation given by composition. They showed that 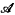is isomorphic to the group of formal power series of the form with group operation given by ‘substitution’ of one power series into another. In particular the most famous ‘cohomology automorphism’, the total Steenrod Square, corresponds to x + x2.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 3 , May 1987 , pp. 469 - 476
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F. and Hirzebruch, F.. Cohomologie-Operationen und charakteristische Klassen. Math. Z. 77 (1961), 149–187.CrossRefGoogle Scholar
[2]Boardman, J. M. and Vogt, R. M.. Homotopy Invariant Algebraic Structures on Topological Spaces. Lecture Notes in Math. vol. 347 (Springer, 1973).CrossRefGoogle Scholar
[3]Dold, A. and Thom, R.. Quasifaserungen und unendliche symmetrische Produkte. Ann. of Math. 67 (1958), 239–281.CrossRefGoogle Scholar
[4]Kozlowski, A.. The transfer in Segal's cohomology. Illinois J. Math. 27 (1983), 614–623.CrossRefGoogle Scholar
[5]May, J. P.. The Geometry of Iterated Loop Spaces. Lecture Notes in Math. vol. 271 (Springer, 1972).CrossRefGoogle Scholar
[6]May, J. P. (with contributions by N. Ray, F. Quinn and J. Tornehave). E∞ Ring Spaces and E∞ Ring Spectra. Lecture Notes in Math. vol. 577 (Springer, 1977).CrossRefGoogle Scholar
[7]May, J. P.. A ∞ ring spaces and algebraic K-theory. In Geometric Applications of Homotopy Theory. Lecture Notes in Math. vol. 656 (Springer, 1978), 240–315.CrossRefGoogle Scholar
[8]Schwanzl, R. and Vogt, R. M.. Homotopy invariance of A ∞ and E ∞ ring spaces. Algebraic Topology, Aarhus 1982. Lecture Notes in Math. vol. 1051 (Springer, 1984), 442–481.CrossRefGoogle Scholar
[9]Segal, G. B.. The multiplicative group of classical cohomology. Quart. J. Math. (2) 26 (1975), 289–293.CrossRefGoogle Scholar
[10]Steiner, R.. Decompositions of groups of units in ordinary cohomology. Quart. J. Math. (2) 30 (1979), 483–494.CrossRefGoogle Scholar