Topological properties of real simple germs, curves, and the nice dimensions n > p
Published online by Cambridge University Press: 24 October 2008
Extract
Infinitesimally stable germs play an important role both as germs from which global C∞-stable mappings are constructed and as germs representing versal unfoldings of (C∞ or holomorphic) germs. Because of the presence of moduli, the C∞ (or analytic) classification of these germs is insufficient and the topological classification of these germs must be understood as well. Here we consider the classification of such germs in the region where no moduli occur. This region is important for several reasons. Most importantly, it contains the infinitesimally stable germs occurring in the nice dimensions. These are the dimensions in which globally infinitesimally stable mappings are dense among the proper C∞-mappings. In (4), it was proved that the topological and C∞-classifications agree for infinitesimally stable germs f: 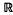 n, 0 →
n, 0 → 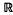 p, 0 in the nice dimensions, n ≤ p. This was then used in (5) to characterize those topologically stable germs which are C∞-stable.
p, 0 in the nice dimensions, n ≤ p. This was then used in (5) to characterize those topologically stable germs which are C∞-stable.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 3 , May 1981 , pp. 457 - 472
- Copyright
- Copyright © Cambridge Philosophical Society 1981
References
REFERENCES
- 5
- Cited by


