Symmetric powers, metabelian Lie powers and torsion in groups

Extract

In this paper we study the homology of groups with coefficients in metabelian Lie powers, and apply the results to obtain information about elements of finite order in certain free central extensions of groups. Perhaps the most prominent example to which our results apply is the relatively free group

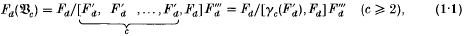
where F_d is the (absolutely) free group of rank d. Thus F_d(B_c) is the free group of rank d in the variety B_c of all groups which are both centre-by-(nilpotent of class ≤ c − 1)-by-abelian and soluble of derived length ≤ 3. It was pointed out in [1] that the order of any torsion element in F_d(B_c) divides c if c is odd and 2c if c is even. This, however, is a conditional result as it does not answer the question of whether or not there are any torsion elements in (1·1). Up to now, this question had only been answered in case when c is a prime number [1] or c = 4 [8]. In these cases F_d (B_c) is torsion-free if d ≤ 3, and elements of finite order do occur in F_d(B_c) if d ≥ 4. Moreover, the torsion elements in F_d(B_c) form a subgroup, and the precise structure of this torsion subgroup was exhibited in [1] in the case when c is a prime and in [8] for c = 4. In the present paper we add to this knowledge. On the one hand, we show that for any prime p dividing c the group F_d(B_c) has no elements of order p for all d up to a certain upper bound, which takes arbitrarily large values as c varies over all multiples of p. On the other hand, we show that for prime powers 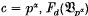does contain elements of order p whenever d ≥ 4. Finally, we exhibit the precise structure of the p-torsion subgroup of 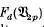when p ≠ 2. Precise statements are given below (Corollaries 1 and 2). Our results on (1·1) are a special case of more general results (Theorems 1′−3′) which refer to a much wider class of groups, and which are, in their turn, a consequence of our main results on the homology of metabelian Lie powers (Theorems 1–3).