Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Le, Huiling
1998.
On the consistency of procrustean mean shapes.
Advances in Applied Probability,
Vol. 30,
Issue. 1,
p.
53.
Kendall, Wilfrid S.
1998.
A diffusion model for bookstein triangle shape.
Advances in Applied Probability,
Vol. 30,
Issue. 2,
p.
317.
Le, Huiling
1998.
On the consistency of procrustean mean shapes.
Advances in Applied Probability,
Vol. 30,
Issue. 1,
p.
53.
Kendall, Wilfrid S.
1998.
A diffusion model for bookstein triangle shape.
Advances in Applied Probability,
Vol. 30,
Issue. 2,
p.
317.
Ball, Frank G.
Dryden, Ian L.
and
Golalizadeh, Mousa
2008.
Brownian Motion and Ornstein–Uhlenbeck Processes in Planar Shape Space.
Methodology and Computing in Applied Probability,
Vol. 10,
Issue. 1,
p.
1.
2016.
Statistical Shape Analysis, with Applications in R.
p.
407.
Cheng, Wen
Dryden, Ian L.
and
Huang, Xianzheng
2016.
Bayesian Registration of Functions and Curves.
Bayesian Analysis,
Vol. 11,
Issue. 2,
Iturriaga, Andrés
Sing Long, Carlos A.
and
Jara, Alejandro
2024.
On dependent Dirichlet processes for general Polish spaces.
Electronic Journal of Statistics,
Vol. 18,
Issue. 1,


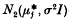 -random points (
-random points (