Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Edmunds, D. E.
and
Webb, J. R. L.
1977.
Some generalizations of the Borsuk–Ulam theorem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 82,
Issue. 1,
p.
119.
NAKAOKA, Minoru
1978.
Equivariant point theorems for involutions.
Japanese journal of mathematics. New series,
Vol. 4,
Issue. 2,
p.
263.
Habegger, Nathan
1986.
On linking coefficients.
Proceedings of the American Mathematical Society,
Vol. 96,
Issue. 2,
p.
353.
Wasserman, Arthur G.
1991.
Isovariant maps and the Borsuk-Ulam theorem.
Topology and its Applications,
Vol. 38,
Issue. 2,
p.
155.
Ахметьев, Петр Михайлович
and
Akhmet'ev, Petr Mikhailovich
2000.
Вложения компактов, стабильные гомотопические группы сфер и теория особенностей.
Успехи математических наук,
Vol. 55,
Issue. 3,
p.
3.
Repovš, Dušan
and
Skopenkov, Arkady
2002.
On projected embeddings and desuspending the α-invariant.
Topology and its Applications,
Vol. 124,
Issue. 1,
p.
69.
Chu, Moody T.
and
Lin, Matthew M.
2024.
On the enumeration of subcells within hypercubes and its application to the Borsuk-Ulam theorem.
Numerical Algorithms,
Vol. 97,
Issue. 2,
p.
595.


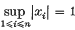 . Let
. Let 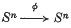 be a piecewise linear (
be a piecewise linear (