Article contents
A simple random walk and an associated asymptotic behaviour of the Bessel functions
Published online by Cambridge University Press: 24 October 2008
Extract
We consider a random walk defined in the following way. We have a set of states indexed by n where n takes on all negative and positive integral values and zero. When we are at state n, there is a probability per unit time λ of going to n + 1, and a probability per unit time λ of going to n − l. Let us start out at n = 0, and study Wn(t), the probability of being at n at time t. Continuity of probability requires that 
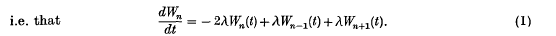

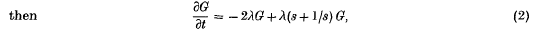 whence since G(s, 0) = 1, we have
whence since G(s, 0) = 1, we have 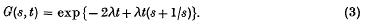 It follows from the well-known result
It follows from the well-known result 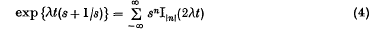
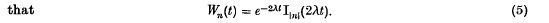 .
.
- Type
- Research Notes
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 4 , October 1962 , pp. 708 - 709
- Copyright
- Copyright © Cambridge Philosophical Society 1962
- 3
- Cited by


