Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T12:52:35.263Z Has data issue: false hasContentIssue false
  • English
  • Français

A robust version of Freiman's 3k–4 Theorem and applications

Published online by Cambridge University Press:  27 March 2018

XUANCHENG SHAO  and
WENQIANG XU
XUANCHENG SHAO
Affiliation:
Department of Mathematics, 715 Patterson Office Tower, University of Kentucky, Lexington, KY, 40506, U.S.A. e-mail: [email protected]
WENQIANG XU
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a robust version of Freiman's 3k – 4 theorem on the restricted sumset A+ΓB, which applies when the doubling constant is at most (3+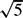$\sqrt{5}$)/2 in general and at most 3 in the special case when A = −B. As applications, we derive robust results with other types of assumptions on popular sums, and structure theorems for sets satisfying almost equalities in discrete and continuous versions of the Riesz–Sobolev inequality.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 166 , Issue 3 , May 2019 , pp. 567 - 581
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by a Glasstone Research Fellowship.

‡

Supported by a London Mathematics Society Undergraduate Research Bursary and the Mathematical Institute at University of Oxford.

References

REFERENCES

[1] Christ, M. An approximate inverse Riesz–Sobolev inequality. arXiv:1112.3715.Google Scholar
[2] Christ, M. Near equality in the Riesz–Sobolev inequality. arXiv:1309.5856.Google Scholar
[3] Christ, M. Near equality in the Riesz–Sobolev inequality in higher dimensions. arXiv:1506.00157.Google Scholar
[4] Christ, M. A sharpened Riesz–Sobolev inequality. arXiv:1706.02007.Google Scholar
[5] Diaconis, P., Shao, X. and Soundararajan, K. Carries, group theory and additive combinatorics. Amer. Math. Monthly 121 (8) (2014), 674–688.10.4169/amer.math.monthly.121.08.674Google Scholar
[6] Lev, V. F. Restricted set addition in groups. III. Integer sumsets with generic restrictions. Period. Math. Hungar. 42 (1-2) (2001), 89–98.10.1023/A:1015248607819Google Scholar
[7] Lev, V. F., Łuczak, T. and Schoen, T. Sum-free sets in abelian groups. Israel J. Math. 125 (2001), 347–367.10.1007/BF02773386Google Scholar
[8] Lev, V. F. and Smeliansky, P. Y. On addition of two distinct sets of integers. Acta Arith. 70 (1) (1995), 85–91.10.4064/aa-70-1-85-91Google Scholar
[9] Lieb, E. H. and Loss, M. Analysis Graduate Studies in Mathematics. vol. 14 (Amer. Math. Soc., Providence, RI, 1997).Google Scholar
[10] Matomäki, K. Real zeros of holomorphic Hecke cusp forms and sieving short intervals. J. Eur. Math. Soc. (JEMS) 18 (1) (2016), 123–146.10.4171/JEMS/585Google Scholar
[11] Mazur, P. A structure theorem for sets of small popular doubling. Acta Arith. 171 (3) (2015), 221–239.10.4064/aa171-3-2Google Scholar
[12] Shao, X. An L-function-free proof of Vinogradov's three primes theorem. Forum Math. Sigma 2 (2014), e27, 26.10.1017/fms.2014.27Google Scholar