No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
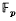,) as a short word in two generatorsPublished online by Cambridge University Press: 24 October 2008
It is one of the first theorems proved in the theory of modular forms [1, p. 78] that every element in SL (2, ℤ), and hence in SL(2, 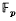), can be written as a product of the two generators
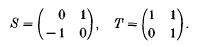
While this is quite an easy result, it required more advanced tools such as spectral analysis on Riemann surfaces [2] to show that there is in fact always such a product of length O(log p). This result is not constructive and therefore immediately [2, p. 102] raises the following:
Problem. Is there an algorithm polynomial in log p for constructing a monomial in S and T, of degree O(log p), whose value is
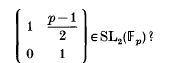
In this note, we construct such an algorithm. We will carry out all the details only for the particular element
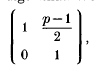
but it will become obvious that our method works for all elements in SL(2, 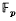).