Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T16:51:54.241Z Has data issue: false hasContentIssue false
  • English
  • Français

On Poincaré's Theorem of “The non-existence of Uniform Integrals of Dynamical Equations”

Published online by Cambridge University Press:  24 October 2008

T. M. Cherry
T. M. Cherry
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

In Chapter v of his Les Méthodes Nouvelles de la Mécanique Céleste Poincaré proves a theorem which he calls The non-existence of Uniform Integrals. This theorem is as follows:

Let

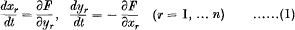
be a system of equations in which the characteristic function F is expanded in a series

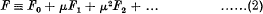
convergent for sufficiently small values of | μ |, for all real values of y1, … yn, and for values of x1, … xn within certain finite real intervals; while F0, F1; … are analytic functions of x1, … xn, y1, … yn, of which F0 is independent of y1, … yn and Fl, F2, … are periodic with respect to these variables with period 2π.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 3 , 20 September 1924 , pp. 287 - 294
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* These intervals are of course to be such that within them the derivatives of F are finite and continuous.

* This statement requires some justification. If P be any point (at which the derivatives of F 0 are finite and continuous) of a space for which x 1, … x n are Cartesian coordinates, we may determine a locus, L 0 say, of the family (10), in which we regard m 1, … m n as continuously variable parameters, to pass through P. Allowing m 1, … m n to vary continuously from their values for L 0, the locus represented by (10) will undergo a continuous displacement in the neighbourhood of P. In any such variation, however small, m 1, … m n simultaneously pass through rational values; thus, since m 1, … m n enter (10) only through their ratios, we can find a locus of the family for which m 1, … m n have integral values, to pass arbitrarily near P.

* Méthodes Nouvelles, § 87.

‡ Acta Math., xxx (1905), 305.Google Scholar

‡ Analytical Dynamics (2nd ed.), p. 385.Google Scholar

§ Phys. Zeit., xxiv (1923), 261Google Scholar.

∥ See, for example, Born, and Pauli, , Zeit. für Phys., x, 137, § 3.Google Scholar

* ‘Integrals of Systems of Ordinary Differential Equations,” p. 273, above.

* If the equations be taken in Poincaré's form (1), the special property of the value μ = 0 is that then the equations simplify in such a far-reaching manner that their solution becomes trivial; we thus reach the paradoxical conclusion that expansions in powers of μ are unsuitable for the precise reason which originally led to their adoption! In fact, as has been remarked by Poincaré, we get into unnecessary difficulties by taking too simple a first approximation; it is this same idea which underlies Gylden's contributions to Celestial Mechanics.

† See p. 281, above.