Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T16:22:42.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the geometrical optics of diffracted wave fronts

Published online by Cambridge University Press:  24 October 2008

F. G. Friedlander
F. G. Friedlander
Affiliation:
The UniversityManchester
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that a solution of the wave equation

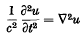
for which u = ∂u/∂t = 0 initially outside a surface S0, vanishes at time t in the exterior of a surface St parallel to, and at normal distance ct from S0, so that the wave fronts of disturbances represented by the solutions of the wave equation obey the laws of geometrical optics. Analogous results hold for the solutions of any linear hyperbolic second-order partial differential equation with boundary value conditions of the ‘Cauchy’ type. But the wave fronts of solutions of problems in which some of the boundary conditions are of the type representing reflexion do not seem to have been treated, and in particular the case of diffraction, when there is a ‘shadow’, does not seem to have been considered at all.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 3 , July 1949 , pp. 395 - 404
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hilbert, D. and Courant, R.Methoden der Mathematischen Physik, 2 (Berlin, 1937), 379.Google Scholar
(2) See, for example, Hadamard, J. Calcul des Variations (Paris, 1910), p. 185.Google Scholar
(3)Bondi, H.Waves on the surface of a compressible liquid. Proc. Cambridge Phil. Soc. 43 (1947), 75–95.CrossRefGoogle Scholar