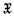Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-02T23:25:21.868Z Has data issue: false hasContentIssue false
  • English
  • Français

-normalizers and 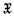-covering subgroups

Published online by Cambridge University Press:  24 October 2008

Mary Jane Prentice
Mary Jane Prentice
Affiliation:
University of Warwick
Get access Rights & Permissions [Opens in a new window]

Extract

In (1), Carter and Hawkes define the -normalizers of a finite soluble group for any saturated formation . These subgroups are conjugate, invariant under homomorphisms of the group, cover and avoid the chief factors of the group and may be characterized by means of the maximal chains of subgroups connecting them to the group. The first aim of the present paper is to generalize both the -normalizers and the relative system normalizers (Hall (5)) of a finite soluble group G. We choose an arbitrary normal subgroup X(p) of G for each prime p dividing the order of G, forming a normal system 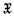= {X(p)} of G. Each of these normal systems 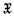of G yields a conjugacy class of subgroups, called the 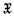-normalizers of G, which possess the above properties of -normalizers. However, they do not satisfy all the properties of the -normalizers unless 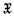is a so-called integrated normal system of G.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 2 , September 1969 , pp. 215 - 230
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Carter, R. and Hawkes, T.The -normalizers of a finite soluble group. J. Algebra 5 (1967), 175–202.CrossRefGoogle Scholar
(2)Gaschütz, W.Uber die Φ-Untergruppe endlicher Gruppen. Math. Z. 58 (1953), 160–170.CrossRefGoogle Scholar
(3)Gaschütz, W.Zur Theorie der endlichen auflösbaren Gruppen. Math. Z. 80 (1963), 300–305.CrossRefGoogle Scholar
(4)Hall, P.On the Sylow systems of a soluble group. Proc. London Math. Soc. (2), 43 (1937), 316–323.Google Scholar
(5)Hall, P.On the system normalizers of a soluble group. Proc. London Math. Soc. (2), 43 (1937), 507–528.Google Scholar
(6)Mann, A.N-normalizers of finite solvable groups. Notices Amer. Math. Soc. (5), 14 (1967), 639.Google Scholar