No CrossRef data available.
Article contents
Maximal prime homomorphic images of mod-p Iwasawa algebras
Published online by Cambridge University Press: 05 March 2021
Abstract
Let k be a finite field of characteristic p, and G a compact p-adic analytic group. Write kG for the completed group ring of G over k. In this paper, we describe the structure of the ring kG/P, where P is a minimal prime ideal of kG. We give an explicit isomorphism between kG/P and a matrix ring with coefficients in the ring 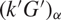 ${(k'G')_\alpha }$
, where
${(k'G')_\alpha }$
, where 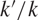 $k'/k$
is a finite field extension,
$k'/k$
is a finite field extension, 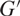 $G'$
is a large subquotient of G with no finite normal subgroups, and (–)α is a “twisting” operation that preserves many desirable properties of the ring structure. We demonstrate the usefulness of this isomorphism by studying the correspondence induced between certain ideals of kG and those of
$G'$
is a large subquotient of G with no finite normal subgroups, and (–)α is a “twisting” operation that preserves many desirable properties of the ring structure. We demonstrate the usefulness of this isomorphism by studying the correspondence induced between certain ideals of kG and those of 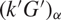 ${(k'G')_\alpha }$
, and showing that this preserves many useful “group-theoretic” properties of ideals, in particular almost-faithfulness and control by a closed normal subgroup.
${(k'G')_\alpha }$
, and showing that this preserves many useful “group-theoretic” properties of ideals, in particular almost-faithfulness and control by a closed normal subgroup.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 2 , September 2021 , pp. 387 - 419
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society


