Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T14:07:36.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Matchings and Radon transforms in lattices II. Concordant sets

Published online by Cambridge University Press:  24 October 2008

Joseph P. S. Kung
Joseph P. S. Kung
Affiliation:
Department of Mathematics, North Texas State University, Denton, TX 76203, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 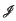and ℳ be subsets of a finite lattice L. 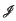is said to be concordant with ℳ if, for every element x in L, either x is in ℳ or there exists an element x+ such that (CS1) the Möbius function μ(x, x+) ≠ 0 and (CS2) for every element j in 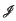, x ∨ j ≠ x+. We prove that if 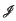is concordant with ℳ, then the incidence matrix I(ℳ | 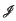) has maximum possible rank |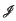|, and hence there exists an injection σ: 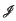→ ℳ such that σ(j) ≥ j for all j in 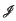. Using this, we derive several rank and covering inequalities in finite lattices. Among the results are generalizations of the Dowling-Wilson inequalities and Dilworth's covering theorem to semimodular lattices, and a refinement of Dilworth's covering theorem for modular lattices.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 2 , March 1987 , pp. 221 - 231
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aigner, M.. Combinatorial Theory (Springer-Verlag, 1979).CrossRefGoogle Scholar
[2]Birkhoff, G.. Lattice Theory, 3rd ed. Amer. Math. Soc. Colloq. Publ., vol. 25 (Amer. Math. Soc, 1967).Google Scholar
[3]Bolker, E.. The finite Radon transform. Proc. Conf. on Integral Geometry, Bowdoin College, 1984 (in the Press).Google Scholar
[4]Dedekind, R.. Über die von drei Moduln erzeugte Dualgruppe. Math. Ann. 53 (1900), 371–403 (= Gesammelte Werke, vol. 2, pp. 236–271).CrossRefGoogle Scholar
[5]Dilworth, R. P.. Proof of a conjecture on finite modular lattices. Ann. Math. (2) 60 (1954), 359–364.CrossRefGoogle Scholar
[6]Doubilet, P.. On the foundations of combinatorial theory. VII. Symmetric functions through the theory of distribution and occupancy. Stud. Appl. Math. 51 (1972), 377–396.CrossRefGoogle Scholar
[7]Dowling, T. A. and Wilson, R. M.. Whitney number inequalities for geometric lattices. Proc. Amer. Math. Soc. 47 (1975), 504–512.CrossRefGoogle Scholar
[8]Ganter, B. and Rival, I.. Dilworth'S covering theorem for modular lattices: A simple proof. Algebra Universalis 3 (1973), 348–350.CrossRefGoogle Scholar
[9]Kung, J. P. S.. The Radon transforms of a combinatorial geometry: I. J. Combin. Theory, Ser. A 26 (1979), 97–102.CrossRefGoogle Scholar
[10]Kung, J. P. S.. Matchings and Radon transforms in lattices. I. Consistent lattices. Order 2 (1985), 105–112.CrossRefGoogle Scholar
[11]Kung, J. P. S.. Radon transforms in combinatorics and lattice theory. In Rival, I. (ed.), Combinatorics and Ordered Sets (Proc. American Mathematical Society Summer Research Conference, Arcata, California, 1985), Contemp. Math., Vol. 57 (American Mathematical Society, 1986), pp. 33–74.CrossRefGoogle Scholar
[12]Kurinnoi, G. C.. A new proof of Dilworth's theorem. Vestnik Char'kov Univ. 93, Mat. Nr. 38 (1973), 11–15 (in Russian).Google Scholar
[13]Reuter, K.. Counting formulas for glued lattices. Order 1 (1985), 265–276.CrossRefGoogle Scholar
[14]Reuter, K. and Rival, I.. Subdiagrams equal in number to their duals. (Preprint.)Google Scholar
[15]Rival, I.. Combinatorial inequalities for semimodular lattices of breadth two. Algebra Universalis 6 (1976), 303–311.CrossRefGoogle Scholar
[16]Rota, G.-C.. On the foundations of combinatorial theory. I. Theory of Möbius functions. Zeit. Wahrsch. Verw. Gebeitel (1964), 340–368.CrossRefGoogle Scholar