Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T03:28:57.539Z Has data issue: false hasContentIssue false
  • English
  • Français

Local uniform and uniform convexity of non-commutative symmetric spaces of measurable operators

Published online by Cambridge University Press:  24 October 2008

Vladimir I. Chilin ,
Andrei V. Krygin  and
Pheodor A. Sukochev
Vladimir I. Chilin
Affiliation:
Department of Mathematics, Tashkent State University, Tashkent 700095, U.S.S.R.
Andrei V. Krygin
Affiliation:
Tashkent Railway Engineering Institute, Tashkent 700045, U.S.S.R.
Pheodor A. Sukochev
Affiliation:
Tashkent Railway Engineering Institute, Tashkent 700045, U.S.S.R.
Get access Rights & Permissions [Opens in a new window]

Extract

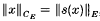Let E be a separable symmetric sequence space, and let CE be the unitary matrix space associated with E, i.e. the Banach space of all compact operators x on l2 so that s(x)E, with the norm , where 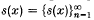are the s-numbers of x. One of the interesting subjects in the theory of the unitary matrix spaces is the clarification of correlation between the geometric properties of the spaces E and CE. A series of results in this direction related with the notions of type, cotype and uniform convexity of the spaces CE has been already obtained (see 13).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 2 , March 1992 , pp. 355 - 368
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Arazy, J.. On the geometry of the unit ball of unitary matrix spaces. Integral Equations Operator Theory 4 (1981), 151171.CrossRefGoogle Scholar
2Garling, D. J. and Tomczak-Jaegermann, N.. The cotype and uniform convexity of unitary ideals. Israel J. Math. 45 (1983), 175197.CrossRefGoogle Scholar
3Tomczak-Jaegermann, N.. Uniform convexity of unitary ideals. Israel J. Math. 48 (1984), 249254.CrossRefGoogle Scholar
4Xu, Q.. Convexit uniforme des spaces symmetriques d'operateurs mesurables. C. R. Acad. Sci. Paris Sr. 1 Math. 309 (1989), 251254.Google Scholar
5Fack, T.. Type and cotype inequalities for non-commutative Lp-spaces. J. Operator Theory 17 (1987), 255279.Google Scholar
6Takesaki, M.. Theory of Operator Algebras, vol. 1 (Springer-Verlag, 1979).CrossRefGoogle Scholar
7Nelson, E.. Notes on non-commutative integration. J. Funct. Anal. 15 (1974), 103116.CrossRefGoogle Scholar
8Fack, T. and Kosaki, . Generalized s-numbers of T-measurable operators. Pacific J. Math. 123 (1986), 269300.CrossRefGoogle Scholar
9Krein, S. G., Petunin, Ju. I. and Semenov, E. M.. Interpolation of Linear Operators (American Mathematical Society, 1982).Google Scholar
10Ovchinnikov, V. I.. Symmetric spaces of measurable operators. Dokl. Akad. Nauk SSSR 191 (1970), 769771.Google Scholar
11Ovchinnikov, V. I.. Symmetric spaces of measurable operators. Trudy NII Matem. VGU 3 (1971), 88107.Google Scholar
12Yeadon, F. J.. Ergodic theorems for semifinite von Neumann algebras II. Math. Proc. Cambridge Philos Soc. 88 (1980), 135147.CrossRefGoogle Scholar
13Dodds, P. G., Dodds, T. K.-Y. and Pagter, B.. Non-commutative Banach function spaces. Math. Z. 201 (1989), 583597.CrossRefGoogle Scholar
14Sukochev, Ph. A. and Chilin, V. I.. Weak Convergence in Non-commutative Symmetric Spaces. Dep. VINITI, no. 2028B90.Google Scholar
15Stinespring, W. F.. Integration theorems for gases and duality for unimodular groups. Trans. Amer. Math. Soc. 90 (1959), 1556.CrossRefGoogle Scholar
16Davis, W. J., Ghossoub, N. and Lindenstrauss, J.. A lattice renorming theorem and applications to vector-valued processes. Trans. Amer. Math. Soc. 263 (1981), 531540.CrossRefGoogle Scholar
17Yeadon, F. J.. Non-commutative Lp-spaces. Math. Proc. Cambridge Philos. Soc. 77 (1975), 91102.CrossRefGoogle Scholar
18Beauzamy, B.. Introduction to Banach Spaces and their Geometry. North-Holland Math. Studies no. 68 (North-Holland, 1982).Google Scholar
19Asplund, E.. Averaged norms. Israel J. Math. 5 (1967), 227233.CrossRefGoogle Scholar
20Lindenstrauss, J. and Tzafriri, L.. Classical Banach Spaces, vol. 2 (Springer-Verlag, 1975).Google Scholar