Published online by Cambridge University Press: 27 April 2011
Let L/K be a finite Galois extension of number fields with Galois group G. We use leading terms of Artin L-series at strictly negative integers to construct elements which we conjecture to lie in the annihilator ideal associated to the Galois action on the higher dimensional algebraic K-groups of the ring of integers in L. For abelian G our conjecture coincides with a conjecture of Snaith and thus generalizes also the well-known Coates–Sinnott conjecture. We show that our conjecture is implied by the appropriate special case of the equivariant Tamagawa number conjecture (ETNC) provided that the Quillen–Lichtenbaum conjecture holds. Moreover, we prove induction results for the ETNC in the case of Tate motives h0(Spec(L))(r), where r is a strictly negative integer. In particular, this implies the ETNC for the pair (h0(Spec(L))(r), 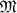 ), where L is totally real, r < 0 is odd and
), where L is totally real, r < 0 is odd and 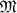 is a maximal order containing ℤ[
is a maximal order containing ℤ[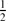 ]G, and will also provide some evidence for our conjecture.
]G, and will also provide some evidence for our conjecture.