Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Greenhow, M.
1986.
High- and low-frequency asymptotic consequences of the Kramers-Kronig relations.
Journal of Engineering Mathematics,
Vol. 20,
Issue. 4,
p.
293.
Miles, John W.
1987.
On surface-wave forcing by a circular disk.
Journal of Fluid Mechanics,
Vol. 175,
Issue. -1,
p.
97.
1989.
Asymptotic Approximations of Integrals.
p.
517.
Stoyanov, B.J.
Farrell, R.A.
and
Bird, J.F.
1994.
Asymptotic expansions of integrals of two Bessel functions via the generalized hypergeometric and Meijer functions.
Journal of Computational and Applied Mathematics,
Vol. 50,
Issue. 1-3,
p.
533.
2006.
Integral Transforms and Their Applications, Second Edition.
p.
673.
Wang, Haiyong
Zhang, Lun
and
Huybrechs, Daan
2013.
Asymptotic expansions and fast computation of oscillatory Hilbert transforms.
Numerische Mathematik,
Vol. 123,
Issue. 4,
p.
709.


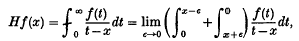
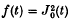 is treated as an example.
is treated as an example.