Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Javaheri, Mohammad
2014.
Hypercyclic and topologically transitive semigroups of composition operators.
Topology and its Applications,
Vol. 164,
Issue. ,
p.
105.
Bonet, José
and
Domański, Paweł
2015.
Abel’s Functional Equation and Eigenvalues of Composition Operators on Spaces of Real Analytic Functions.
Integral Equations and Operator Theory,
Vol. 81,
Issue. 4,
p.
455.
Zajac, Sylwester
2016.
Hypercyclicity of composition operators in Stein manifolds.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 9,
p.
3991.
Bonet, José
and
Domański, Paweł
2017.
A Note on the Spectrum of Composition Operators on Spaces of Real Analytic Functions.
Complex Analysis and Operator Theory,
Vol. 11,
Issue. 1,
p.
161.
PENG, Liangxue
and
YANG, Chong
2017.
A note on dynamics in functional spaces.
TURKISH JOURNAL OF MATHEMATICS,
Vol. 41,
Issue. ,
p.
186.
Przestacki, A.
2017.
Dynamical properties of weighted composition operators on the space of smooth functions.
Journal of Mathematical Analysis and Applications,
Vol. 445,
Issue. 1,
p.
1097.
Yin, Zongbin
2017.
Chaotic Dynamics of Composition Operators on the Space of Continuous Functions.
International Journal of Bifurcation and Chaos,
Vol. 27,
Issue. 06,
p.
1750084.
Bès, J.
Conejero, J.A.
and
Papathanasiou, D.
2018.
Hypercyclic algebras for convolution and composition operators.
Journal of Functional Analysis,
Vol. 274,
Issue. 10,
p.
2884.
Yin, Zongbin
Chen, Yuming
and
He, Shengnan
2018.
Disjoint Hypercyclicity and Topological Entropy of Composition Operators.
International Journal of Bifurcation and Chaos,
Vol. 28,
Issue. 04,
p.
1850053.
Colonna, Flavia
and
Martínez-Avendaño, Rubén A.
2018.
Hypercyclicity of Composition Operators on Banach Spaces of Analytic Functions.
Complex Analysis and Operator Theory,
Vol. 12,
Issue. 1,
p.
305.
Fernández, Carmen
Galbis, Antonio
and
Jordá, Enrique
2018.
Dynamics and spectra of composition operators on the Schwartz space.
Journal of Functional Analysis,
Vol. 274,
Issue. 12,
p.
3503.
Peris, Alfred
2018.
A hypercyclicity criterion for non-metrizable topological vector spaces.
Functiones et Approximatio Commentarii Mathematici,
Vol. 59,
Issue. 2,
Goliński, Michał
and
Przestacki, Adam
2020.
Dynamical properties of weighted translation operators on the Schwartz space $$\mathcal {S}(\mathbb {R})$$S(R).
Revista Matemática Complutense,
Vol. 33,
Issue. 1,
p.
103.
Piszczek, Krzysztof
and
Przestacki, Adam
2021.
Frequent hypercyclicity of weighted composition operators on the space of smooth functions.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 2,
Zhang, Li
Zhou, Zehua
Zhang, Liang
and
Lu, Huiqiang
2022.
Notes on Hypercyclicity of Composition Operator on the Weighted Dirichlet Spaces.
Complex Analysis and Operator Theory,
Vol. 16,
Issue. 6,
Albanese, Angela A.
Jordá, Enrique
and
Mele, Claudio
2022.
Dynamics of composition operators on function spaces defined by local and global properties.
Journal of Mathematical Analysis and Applications,
Vol. 514,
Issue. 1,
p.
126303.
Yang, Qigui
and
Xiang, Qiaomin
2022.
Chaotic vibrations of 3D linear hyperbolic PDEs with linear perturbations of superlinear boundary conditions.
Journal of Mathematical Analysis and Applications,
Vol. 507,
Issue. 1,
p.
125743.
Almohammedali, Fadelah
and
Chan, Kit C.
2023.
Hypercyclic composition operators with automorphisms of the upper half-plane.
Journal of Mathematical Analysis and Applications,
Vol. 519,
Issue. 1,
p.
126745.
Kalmes, Thomas
and
Przestacki, Adam
2024.
Hypercyclic and mixing composition operators on $${\mathscr {O}}_M({\mathbb {R}})$$.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 4,
Bernardes, Nilson C.
Caraballo, Blas M.
Darji, Udayan B.
Fávaro, Vinícius V.
and
Peris, Alfred
2025.
Generalized hyperbolicity, stability and expansivity for operators on locally convex spaces.
Journal of Functional Analysis,
Vol. 288,
Issue. 2,
p.
110696.
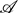 (Ω) of real analytic functions on an open subset Ω of ℝd. We characterize when such operators are topologically transitive, i.e. when for every pair of non-empty open sets there is an orbit intersecting both of them. Moreover, under mild assumptions on the composition operator, we investigate when it is sequentially hypercyclic, i.e., when it has a sequentially dense orbit. If ϕ is a self map on a simply connected complex neighbourhood U of ℝ, U ≠ ℂ, then topological transitivity, hypercyclicity and sequential hypercyclicity of Cϕ:
(Ω) of real analytic functions on an open subset Ω of ℝd. We characterize when such operators are topologically transitive, i.e. when for every pair of non-empty open sets there is an orbit intersecting both of them. Moreover, under mild assumptions on the composition operator, we investigate when it is sequentially hypercyclic, i.e., when it has a sequentially dense orbit. If ϕ is a self map on a simply connected complex neighbourhood U of ℝ, U ≠ ℂ, then topological transitivity, hypercyclicity and sequential hypercyclicity of Cϕ: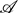 (ℝ) →
(ℝ) → 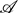 (ℝ) are equivalent.
(ℝ) are equivalent.