Hopf algebras and regular isotopy invariants for link diagrams
Published online by Cambridge University Press: 24 October 2008
Extract
In this paper, we shall consider the following method for obtaining regular isotopy invariants of link diagrams. Given any link diagram L, equip it with a Morse function h, so that the diagram consists entirely of crossings, maxima, minima and vertical arcs. Introduce 2-valent graphical vertices to separate the various segments of the diagram. Given a finite index set I, a state σ for Lh is an assignation of one element of I to each graphical vertex. Each segment of the diagram now has a weight
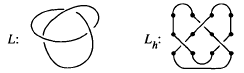
associated with it, given in terms of tensor coordinates indexed by the set I by the pictures
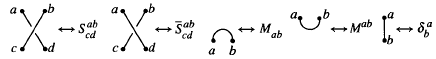
and, for any state σ, [Li|σ] denotes the product of the various weights. We then define 〈Lh〉 to be the sum of [Lh|σ] over all possible states σ,
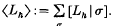
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 1 , January 1991 , pp. 59 - 77
- Copyright
- Copyright © Cambridge Philosophical Society 1991
References
REFERENCES
- 4
- Cited by


