Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
González-Dávila, J. C.
and
Martín Cabrera, F.
2011.
Harmonic almost contact structures via the intrinsic torsion.
Israel Journal of Mathematics,
Vol. 181,
Issue. 1,
p.
145.
Dávila, J. C. González
and
Cabrera, F. Martín
2012.
Homogeneous nearly Kähler manifolds.
Annals of Global Analysis and Geometry,
Vol. 42,
Issue. 2,
p.
147.
González-Dávila, J.C.
2016.
Energy of generalized distributions.
Differential Geometry and its Applications,
Vol. 49,
Issue. ,
p.
510.
Niedziałomski, Kamil
2018.
Examples of Minimal
$$\varvec{G}$$
G
-structures.
Results in Mathematics,
Vol. 73,
Issue. 2,
González-Dávila, José Carmelo
2018.
Harmonicity and minimality of complex and quaternionic radial foliations.
Forum Mathematicum,
Vol. 30,
Issue. 3,
p.
785.
Niedziałomski, Kamil
2020.
Harmonic SU(3)- and $$G_2$$-Structures via Spinors.
Results in Mathematics,
Vol. 75,
Issue. 3,
Martín Cabrera, Francisco
2020.
The exterior derivative of the Lee form of almost Hermitian manifolds.
Journal of Geometry and Physics,
Vol. 148,
Issue. ,
p.
103563.
Niedziałomski, Kamil
2022.
An integral formula for G2–structures.
Journal of Geometry and Physics,
Vol. 176,
Issue. ,
p.
104511.
Moreno, Andrés J.
2023.
Harmonic G2-structures on almost Abelian Lie groups.
Differential Geometry and its Applications,
Vol. 91,
Issue. ,
p.
102060.
Loubeau, Eric
and
Sá Earp, Henrique N.
2023.
Harmonic flow of geometric structures.
Annals of Global Analysis and Geometry,
Vol. 64,
Issue. 4,
Ferraris, Francisco
Moas, Ruth Paola
and
Salvai, Marcos
2023.
Harmonic unit normal sections of Grassmannians associated with cross products.
Revista Matemática Complutense,
Vol. 36,
Issue. 2,
p.
443.
Andrada, Adrián
and
Tolcachier, Alejandro
2024.
Harmonic Complex Structures and Special Hermitian Metrics on Products of Sasakian Manifolds.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 6,
Niedziałomski, Kamil
2024.
A type of nearly parallel G-structures.
Journal of Geometry and Physics,
Vol. 203,
Issue. ,
p.
105256.
Andrada, Adrián
and
Tolcachier, Alejandro
2024.
Harmonic almost complex structures on almost abelian Lie groups and solvmanifolds.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 203,
Issue. 3,
p.
1037.
Fadel, Daniel
Loubeau, Eric
Moreno, Andrés J.
and
Sá Earp, Henrique N.
2024.
Flows of geometric structures.
Journal für die reine und angewandte Mathematik (Crelles Journal),
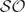 (M)/G. We deduce the corresponding first and second variation formulae and the characterising conditions for critical points by means of tools closely related to the study of G-structures. In this direction, we show the rôle in the energy functional played by the intrinsic torsion of the G-structure. Moreover, we analyse the particular case G=U(n) for 2n-dimensional manifolds. This leads to the study of harmonic almost Hermitian manifolds and harmonic maps from M into
(M)/G. We deduce the corresponding first and second variation formulae and the characterising conditions for critical points by means of tools closely related to the study of G-structures. In this direction, we show the rôle in the energy functional played by the intrinsic torsion of the G-structure. Moreover, we analyse the particular case G=U(n) for 2n-dimensional manifolds. This leads to the study of harmonic almost Hermitian manifolds and harmonic maps from M into 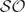 (M)/U(n).
(M)/U(n).