Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T02:19:21.156Z Has data issue: false hasContentIssue false
  • English
  • Français

Finiteness and decidability: II

Published online by Cambridge University Press:  24 October 2008

P. T. Johnstone  and
F. E. J. Linton
P. T. Johnstone
Affiliation:
University of Cambridge, England
F. E. J. Linton
Affiliation:
Wesleyan University, Middletown, Conn., U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

It has been known for some time ((6), p. 270; (4), theorem 9·19) that if 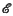is a Boolean topos, then the full subcategory 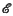Kf of Kuratowski-finite objects in 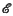is again a topos. For a non-Boolean topos 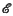, however, 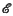Kf need not be a topos, as can be seen when 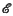is the Sierpinski topos ((1), example 7·1); on the other hand, two other full subcategories of 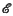, coinciding with 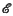Kf when 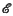is Boolean, suggest themselves as candidates for a subtopos of finite objects. Of one of these, the category 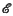dKf of decidable K-finite objects in 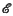, the Main Theorem of (1) asserts that it is always a (Boolean) topos. The other is the category 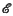sKf of 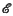-subobjects of K-finite objects. The inclusions

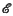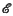dKf ⊆ Kf ⊆ 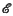sKf are clear.

are clear.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 84 , Issue 2 , September 1978 , pp. 207 - 218
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Acuña-Ortega, O. and Linton, F. E. J. Finiteness and decidability: I. Proc. L.M.S. Durham symposium on applications of sheaf theory (Springer Lecture Notes in Mathematics, to appear).Google Scholar
(2)Dummett, M. A. E.Elements of intuitionism (Oxford Logic Guides; Oxford: Clarendon Press, 1977).Google Scholar
(3)Engenes, H.Subobject classifiers and classes of subfunctors. Math. Scand. 34 (1974), 145–152.Google Scholar
(4)Johnstone, P. T.Topos theory (L.M.S. Mathematical Monographs no. 10; London: Academic Press, 1977).Google Scholar
(5)Johnstone, P. T. Conditions related to De Morgan's law. Proc. L.M.S. Durham symposium on applications on sheaf theory (Springer Lecture Notes in Mathematics, to appear).Google Scholar
(6)Kock, A., Lecouturier, P. and Mikkelsen, C. J.Some topos-theoretic concepts of finiteness. In Model theory and Topoi, pp. 209–283 (Springer Lecture Notes in Mathematics, no. 445, 1975).CrossRefGoogle Scholar
(7)Lawvere, F. W. Quantifiers and sheaves. In Actes du Congrès Intern. des Math., Nice 1970, tome 1, pp. 329–334 (Paris: Gauthier–Villars, 1971).Google Scholar