Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2025-01-01T16:40:23.953Z Has data issue: false hasContentIssue false
  • English
  • Français

Discontinuous homomorphisms from Banach *-algebras

Published online by Cambridge University Press:  24 October 2008

Volker Runde
Volker Runde
Affiliation:
Fachbereich 9 Mathematik, Universität des Saarlandes, Postfach 151150, 66041 Saarbrücken, Germany e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The long open problem raised by I. Kaplansky if, for an infinite compact Hausdorff space X, there is a discontinuous homomorphism from 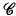(X) into a Banach algebra was settled in the 1970s, independently, by H. G. Dales and J. Esterle. If the continuum hypothesis is assumed, then there is a discontinuous homomorphism from 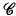(X) (see [8] for a survey of both approaches and [9] for a unified exposition). The techniques developed by Dales and Esterle are powerful enough to yield discontinuous homomorphisms from commutative Banach algebras other than 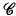(X). In fact, every commutative Banach algebra with infinitely many characters is the domain of a discontinuous homomorphism ([7]).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 4 , November 1996 , pp. 703 - 708
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Albrecht, E. and Dales, H. G.. Continuity of homomorphisms from C*-algebras and other Banach algebras; in Bachar, J. M. et al. (eds.), Radical Banach algebras and automatic continuity (Springer Verlag, 1983), pp. 375–396.CrossRefGoogle Scholar
[2]Barnes, B. A.. Ideal and representation theory of the L 1-algebra of a group with polynomial growth. Coll. Math. XLV (1981), 301–315.CrossRefGoogle Scholar
[3]Barnes, B. A.. The properties *-regularity and uniqueness of C*-norm in a general *-algebra. Trans. Amer. Math. Soc. 279 (1983), 841–859.Google Scholar
[4]Boidol, J., Leptin, H., Schürmann, J. and Vahle, D.. Räume primitiver Ideale von Gruppenalgebren. Math. Ann. 236 (1978), 1–13.CrossRefGoogle Scholar
[5]Bonsall, F. F. and Duncan, J.. Complete normed algebras (Springer Verlag, 1973).CrossRefGoogle Scholar
[6]Conway, J. B.. A course in functional analysis (Springer Verlag, 1985).CrossRefGoogle Scholar
[7]Dales, H. G.. Discontinuous homomorphisms from topological algebras. Amer. J. Math. 101 (1976), 635–646.CrossRefGoogle Scholar
[8]Dales, H. G.. Automatic continuity: a survey. Bull. London Math. Soc. 10 (1978), 129–183.CrossRefGoogle Scholar
[9]Dales, H. G.. Banach algebras and automatic continuity (Oxford University Press, in preparation).CrossRefGoogle Scholar
[10]Dixmier, J.. C*-algebras (translated from the French) (North-Holland, 1977).Google Scholar
[11]Ermert, O.. Continuity of homomorphisms from AF-C*-algebras and other inductive limit C*-algebras. J. London Math. Soc., to appear.Google Scholar
[12]Hewitt, E. and Ross, K. A.. Abstract harmonic analysis, II (Springer Verlag, 1970).Google Scholar
[13]Jacobson, N.. Structure of rings (American Mathematical Society, 1964).Google Scholar
[14]Kaniuth, E.. *-regularity of locally compact groups; in Heyer, H. (ed.), Probability measures on groups, VII (Springer Verlag, 1984), pp. 235–240.CrossRefGoogle Scholar
[15]Loomis, L. H.. An introduction to abstract harmonic analysis (Van Nostrand, 1953).Google Scholar
[16]McCoy, N. H.. The theory of rings (MacMillan, 1964).Google Scholar
[17]Runde, V.. Homomorphisms from L 1(G) for G є [FIA]- U [Moore]. J. Fund. Anal. 122 (1994), 25–51.CrossRefGoogle Scholar
[18]Runde, V.. When is there a discontinuous homomorphism from L 1 (G)? Studia Math. 110 (1994), 97–104.CrossRefGoogle Scholar