Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T13:50:00.735Z Has data issue: false hasContentIssue false
  • English
  • Français

Conformally Kähler manifolds*

Published online by Cambridge University Press:  24 October 2008

W. J. Westlake
W. J. Westlake
Affiliation:
37 Sydenham Villas Road Cheltenham
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. The present paper is concerned with the conformal geometry of Hermitian spaces. In the first part we find a necessary and sufficient condition for a Hermitian space to be conformally Kähler, that is, conformal to some Kähler space. The condition is that a certain conformal tensor, 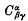, vanishes identically. Then, defining a Hermitian manifold as in Hodge (3), we consider such a manifold where the restriction is made that at every point the tensor 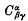is zero. This will be called a conformally Kähler manifold, and conditions under which it may be given a Kähler metric are obtained. It is found that any conformally Kähler manifold may be given a Kähler metric provided it is simply-connected or that its fundamental group is of finite order.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 1 , January 1954 , pp. 16 - 19
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Coburn, N.Conformal unitary spaces. Trans. Amer. math. Soc. 50 (1941), 26–39.Google Scholar
(2)Eckmann, B. and Guggenheimer, H.Various closes de métrique hermitienne sans torsione. C.R. Acad. Sci., Paris, 229 (1949), 503–5.Google Scholar
(3)Hodge, W. V. D.A special type of Kähler manifold. Proc. Lond. math. Soc. (3), 1 (1951), 104–17.CrossRefGoogle Scholar
(4)Kuiper, N.On conformally flat spaces in the large. Ann. Math., Princeton, 50 (1949), 916–24.Google Scholar
(5)Schouten, J. A. and Struik, D. J.Einführung in die neueren Methoden der Differentialgeometric (2) (Groningen, 1938).Google Scholar