Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T16:12:41.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Changes of signs of restrictions of Fourier–Stieltjes transforms

Published online by Cambridge University Press:  24 October 2008

G. I. Gaudry
G. I. Gaudry
Affiliation:
University of Warwick, Coventry
Get access Rights & Permissions [Opens in a new window]

Abstract

Our principal result deals with a function φ defined on the ‘non-negative half’ X+ of a discrete ordered group X, the dual of a compact Abelian connected group G. Suppose φ vanishes outside a countable set S = {χ1, χ2 …} and has the following property: for every t in a set 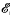0 ⊂ (0, 1) of positive Lebesgue measure, the function on X+ defined to be 0 off S and to be rn(t)φ(χn) for χ = χn, where rn is the nth Rademacher function, is the restriction to X+ of a Fourier–Stieltjes transform. We conclude that φ ∈ ℓ2(X+).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 2 , September 1969 , pp. 295 - 300
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Edwards, R. E.Functional analysis: theory and applications (Holt, Rinehart and Winston; New York, 1965).Google Scholar
(2)Edwards, R. E.Changing signs of Fourier coefficients. Pacific J. Math. 15 (1965), 463–475.CrossRefGoogle Scholar
(3)Figà-Talamanca, , Alessandro, and Rider, , Daniel, A theorem on random Fourier series on non commutative groups. Pacific J. Math. 21 (1967), 487–492.CrossRefGoogle Scholar
(4)Gaudry, G. I.Hp multipliers and inequalities of Hardy and Littlewood. To appear J. Austral. Math. Soc.Google Scholar
(5)Helson, , Henry, . Conjugate series and a theorem of Paley. Pacific J. Math. 8 (1958), 437–446.CrossRefGoogle Scholar
(6)Rudin, , Walter, . Fourier analysis on groups (Interscience; New York, 1962).Google Scholar
(7)Sidon, S.Ein Satz über Fouriersche Eeihen stetiger Funktionen. Math. Z. 32 (1932), 485–486.CrossRefGoogle Scholar
(8)Zygmund, , Antoni, . Trigonometric series, vol. I (Cambridge, 1959).Google Scholar