Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T10:58:18.706Z Has data issue: false hasContentIssue false
  • English
  • Français

The algebra of parallel endomorphisms of a pseudo-Riemannian metric: semi-simple part

Published online by Cambridge University Press:  19 June 2015

CHARLES BOUBEL
CHARLES BOUBEL*
Affiliation:
Institut de Recherche Mathématique Avancée, UMR 7501 – Université de Strasbourg et CNRS, 7 rue René Descartes, 67084 Strasbourg Cedex, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

On a (pseudo-)Riemannian manifold (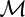${\mathcal M}$, g), some fields of endomorphisms i.e. sections of End(T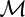${\mathcal M}$) may be parallel for g. They form an associative algebra 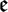$\mathfrak e$, which is also the commutant of the holonomy group of g. As any associative algebra, 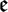$\mathfrak e$ is the sum of its radical and of a semi-simple algebra 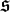$\mathfrak s$. Here we study 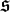$\mathfrak s$: it may be of eight different types, including the generic type 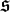$\mathfrak s$ = ${\mathbb R}$ Id, and the Kähler and hyperkähler types 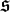$\mathfrak s$ ≃ 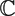${\mathbb C}$ and 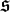$\mathfrak s$ ≃ ${\mathbb H}$. This is a result on real, semi-simple algebras with involution. For each type, the corresponding set of germs of metrics is non-empty; we parametrize it. We give the constraints imposed to the Ricci curvature by parallel endomorphism fields.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 219 - 237
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bérard–Bergery, L. and Ikemakhen, A. Sur l'holonomie des varié-tés pseudo-Riemanniennes de signature (n, n). Bull. Soc. Math. France 125 no. 1 (1997), 93–114.Google Scholar
[2] Boubel, C. The algebra of the parallel endomorphisms of a germ of pseudo-Riemannian metric. J. Differential Geom. 99 No. 1 (2015), 77–123.Google Scholar
[3] Boubel, C. and Bérard–Bergery, L. On pseudo-Riemannian manifolds whose Ricci tensor is parallel. Geom. Dedicata 86 No. 1–3 (2001), 1–18.Google Scholar
[4] Bourbaki, N. Éléments de mathématique. Livre II: Algèbre. Chap. 8: Modules et anneaux semisimples. (French) Actualités scientifiques et industrielles (Hermann, 1958).Google Scholar
[5] Bryant, R. Metrics with exceptional holonomy. Ann. Math. 126 (1987), 525–576.Google Scholar
[6] Bryant, R. L., Chern, S. S., Gardner, R. B., Goldschmidt, H. L. and Griffiths, P. A. Exterior differential systems. Math. Sci. Res. Inst. Publ., 18 (Springer-Verlag, 1991).Google Scholar
[7] Bryant, R. Classical, exceptional, and exotic holonomies: A status report. In: Besse, A. (Ed.), Actes de la table ronde de géométrie différentielle en l'honneur de Marcel Berger, Luminy, France (12–18 juillet, 1992), Société Mathématique de France, Sémin. Congr., 1 (1996), 93–165.Google Scholar
[8] Bryant, R. Bochner-Kähler metrics, J. Amer. Math. Soc. 14, No. 3 (2001), 623–715.Google Scholar
[9] Curtis, C. and Reiner, I. Representation theory of finite groups and associative algebras. Reprint of the 1962 original (AMS Chelsea Publishing, 2006).Google Scholar
[10] Galaev, A. and Leistner, T. Recent developments in pseudo-Riemannian holonomy theory. In: Handbook of pseudo-Riemannian geometry and supersymmetry. IRMA Lect. Math. Theor. Phys., 16 (Eur. Math. Soc. 2010), 581–627.Google Scholar
[11] Ghanam, R. and Thompson, G. The holonomy Lie algebras of neutral metrics in dimension four. J. Math. Phys. 42 no. 5 (2001), 2266–2284.Google Scholar
[12] Ivey, T. A. and Landsberg, J. M. Cartan for beginners: differential geometry via moving frames and exterior differential systems. Graduate Studies in Mathematics, 61 Amer. Math. Soc. (2003).Google Scholar
[13] Jacobson, N. Structure of rings. Amer. Math. Soc. Colloquium Publications, vol. 37 (1956).Google Scholar
[14] Milnor, J. Morse theory. Based on lecture notes by Spivak, M. and Wells, R. Ann. of Math. Stud. no. 51 (Princeton University Press, 1963).Google Scholar
[15] Moroianu, A. Lectures on Kähler Geometry (Cambridge University Press, 2007).Google Scholar
[16] Schwachhöfer, L. Connections with irreducible holonomy representations. Adv. Math. 160 No. 1 (2001), 1–80.Google Scholar
[17] Taft, E. J. Invariant Wedderburn factors. Illinois J. Math. 1 (1957), 565–573.Google Scholar
[18] Taft, E. J. Cleft algebras with operator groups. Portugal. Math. 20 (1961), 195–198.Google Scholar