Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T01:20:37.414Z Has data issue: false hasContentIssue false
  • English
  • Français

The wave front set of the solution of a simple initial-boundary value problem with glancing rays. II

Published online by Cambridge University Press:  24 October 2008

F. G. Friedlander  and
R. B. Melrose
F. G. Friedlander
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Cambridge
R. B. Melrose
Affiliation:
St John's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a sequel to an earlier paper in these Proceedings by one of us ((5); this will be referred to as [I]). The question considered there was that of determining the wave front set of the solution of the boundary value problem

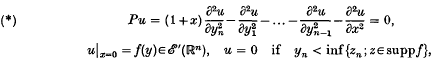
where x∈+, y∈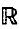n, and n > 1; the precise meaning of the boundary condition at x = 0 is explained in section 1 below. The principal result of [I] can be expressed concisely by saying that singularities do not propagate along the boundary; a detailed statement is given in Theorem 1·9 of the present paper.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 81 , Issue 1 , January 1977 , pp. 97 - 120
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Andersson, K. G.Propagation of analyticity of solutions of partial differential equations with constant coefficients. Ark. Mat. 8 (1971), 277–302.CrossRefGoogle Scholar
(2)Andersson, K. G.Analytic wave front sets for solutions of linear differential equations of principal type. Trans. Amer. Math. Soc. 177 (1973), 1–27.Google Scholar
(3)Atiyah, M. F., Bott, R. and Gårding, L.Lacunas for hyperbolic differential operators with constant coefficients: I. Acta Math. 124 (1970), 109–189.Google Scholar
(4)Boutet de Monvel, L. and Krée, P. Pseudo-differential operators and Gevrey classes. Ann. Inst. Fourier (Grenoble) 17 (1967), 295–323.Google Scholar
(5)Friedlander, F. G.The wave front set of the solution of a simple initial-boundary value problem with glancing rays. Math. Proc. Cambridge Philos. Soc. 79 (1976), 145–159.CrossRefGoogle Scholar
(6)Hörmander, L.Uniqueness theorems and wave front sets for solutions of linear differential equations with analytic coefficients. Comm. Pure Appl. Math. 24 (1971), 671–703.CrossRefGoogle Scholar
(7)Hörmander, L.Linear partial differential operators (Springer, 1963).CrossRefGoogle Scholar
(8)Hörmander, L.On the existence and regularity of solutions of linear pseudo-differential equations. Enseignement Math. 17 (1971), 99–163.Google Scholar
(9)Hörmander, L.Fourier integral operators: I. Acta Math. 127 (1971), 79–183.Google Scholar
(10)Melrose, R. B.Microlocal parametrices for diffractive boundary value problems. Duke Math. J. 42 (1975), 605–635.Google Scholar
(11)Melrose, R. B.Equivalence of glancing hypersurfaces. Invent. Math, (to appear).Google Scholar
(12)Oshima, T.Sato's problem in contact geometry (manuscript, 1976).Google Scholar
(13)Sato, M., Kawai, T. and Kashiwara, M. Microfunctions and pseudo-differential equations. Lecture Notes in Math. (Springer) 287 (1973), 265–529.Google Scholar
(14)Schwartz, L.Théorie des distributions (Paris, Hermann, 1966).Google Scholar
(15)Seeley, R. T.Extension of C ∞ functions defined in a half space, Proc. Amer. Math. Soc. 15 (1964), 625–626.Google Scholar
(16)Taylor, M. E.Grazing rays and reflexion of singularities of solutions to wave equations. Comm. Pure Appl. Math. 29 (1976), 1–38.CrossRefGoogle Scholar