Published online by Cambridge University Press: 24 October 2008
Professor H. Davenport has raised the following question. Let f(X) be a homogeneous form in n variables X, of degree k, with coefficients in a field K. Is it possible to write f(X) in the form
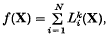
where the Li(X) are linear forms over K and N depends only on K, n, and k? In particular, what can be said when K = R, the reals; K = Q, the rationals; K = C, the complex numbers ?
We shall show that when k is odd such a representation is always possible and we shall obtain an explicit bound for N. However, if k is even, no such result is possible when K = R or Q, even when we impose the obvious necessary condition that f(X) be positive semi-definite. In fact we shall exhibit a construction for obtaining forms f(X) which are positive definite but cannot be expressed in the form
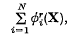
r even, where φi(X) is a homogeneous form of degree s and sr = k. We shall determine precisely which definite forms can be expressed in the required form. Some natural generalizations of the problem are then considered.