Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:50:26.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Triforce and corners

Part of: Sequences and sets Extremal combinatorics

Published online by Cambridge University Press:  12 July 2019

JACOB FOX ,
ASHWIN SAH ,
MEHTAAB SAWHNEY ,
DAVID STONER  and
YUFEI ZHAO
JACOB FOX
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, U.S.A. e-mail: [email protected]
ASHWIN SAH
Affiliation:
Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A. e-mail: [email protected], [email protected]
MEHTAAB SAWHNEY
Affiliation:
Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A. e-mail: [email protected], [email protected]
DAVID STONER
Affiliation:
Harvard University, Cambridge, MA 02138, U.S.A. e-mail: [email protected]
YUFEI ZHAO
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

May the triforce be the 3-uniform hypergraph on six vertices with edges {123′, 12′3, 1′23}. We show that the minimum triforce density in a 3-uniform hypergraph of edge density δ is δ4–o(1) but not O(δ4).

Let M(δ) be the maximum number such that the following holds: for every ∊ > 0 and 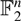$G = {\mathbb{F}}_2^n$ with n sufficiently large, if A ⊆ G × G with A ≥ δ|G|2, then there exists a nonzero “popular difference” d ∈ G such that the number of “corners” (x, y), (x + d, y), (x, y + d) ∈ A is at least (M(δ)–∊)|G|2. As a corollary via a recent result of Mandache, we conclude that M(δ) = δ4–o(1) and M(δ) = ω(δ4).

On the other hand, for 0 < δ < 1/2 and sufficiently large N, there exists A ⊆ [N]3 with |A| ≥ δN3 such that for every d ≠ 0, the number of corners (x, y, z), (x + d, y, z), (x, y + d, z), (x, y, z + d) ∈ A is at most δc log(1/δ)N3. A similar bound holds in higher dimensions, or for any configuration with at least 5 points or affine dimension at least 3.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 05D05: Extremal set theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 1 , July 2020 , pp. 209 - 223
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by a Packard Fellowship and NSF Career Award DMS-1352121

‡

Supported by NSF Award DMS-1764176, and the MIT Solomon Buchsbaum Fund

References

REFERENCES

Ajtai, M. and SzemeréDi, E.. Sets of lattice points that form no squares. Stud. Sci. Math. Hungar. 9 (1974), 9–11.Google Scholar
Alon, N.. Testing subgraphs in large graphs. Random Structures Algorithms 21 (2002), 359–370.CrossRefGoogle Scholar
Behrend, F. A.. On sets of integers which contain no three terms in arithmetical progression. Proc. Natl. Acad. Sci. USA 32 (1946), 331–332.CrossRefGoogle ScholarPubMed
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences, with an appendix by Imre Ruzsa. Invent. Math. 160 (2005), 261–303.CrossRefGoogle Scholar
Chu, Q.. Multiple recurrence for two commuting transformations. Ergodic Theory Dynam. Systems 31 (2011), 771–792.CrossRefGoogle Scholar
Elek, G. and Szegedy, B.. A measure-theoretic approach to the theory of dense hypergraphs. Adv. Math. 231 (2012), 1731–1772.CrossRefGoogle Scholar
Fox, J. and Pham, H. T.. Popular progression differences in vector spaces. Int. Math. Res. Not. IMRN, to appear.Google Scholar
Fox, J. and Pham, H. T.. Popular progression differences in vector spaces II. Discrete Anal., to appear.Google Scholar
Fox, J., Pham, H. T., and Zhao, Y.. Tower-type bounds for Roth’s theorem with popular differences. Preprint.Google Scholar
Green, B.. A Szemerédi-type regularity lemma in abelian groups, with applications. Geom. Funct. Anal. 15 (2005), 340–376.CrossRefGoogle Scholar
Green, B.. Some open problems, manuscript.Google Scholar
Green, B. and Tao, T.. An arithmetic regularity lemma, an associated counting lemma, and applications. In An Irregular Mind (Szemerédi is 70) (ed. I. Bárány, J. Solymosi, G. Sági), 261–334 (Springer, Berlin, Heidelberg), 2010.CrossRefGoogle Scholar
LováSz, L. and Szegedy, B.. Szemerédi’s lemma for the analyst. Geom. Funct. Anal. 17 (2007), 252–270.CrossRefGoogle Scholar
Mandache, M.. A variant of the corner theorem. Preprint, arXiv:1804.03972.Google Scholar
Nair, M.. On Chebyshev-type inequalities for primes. Amer. Math. Monthly 89 (1982), 126–129.CrossRefGoogle Scholar
Roth, K. F.. On certain sets of integers. J. London Math. Soc. 28 (1953), 104–109.CrossRefGoogle Scholar
Ruzsa, I. Z. and SzemeréDi, E.. Triple systems with no six points carrying three triangles. In Combinatorics (Keszthely, 1976), Coll. Math. Soc. J. Bolyai 18, Volume II, 939–945.Google Scholar
Schoen, T. and Sisask, O.. Roth’s theorem for four variables and additive structures in sums of sparse sets. Forum Math. Sigma 4 (2016), e5, 28pp.CrossRefGoogle Scholar
Solymosi, J.. Note on a generalization of Roth’s theorem. In Discrete and computational geometry, Algorithms Combin. vol. 25 (Springer, 2003), 825–827.CrossRefGoogle Scholar
Solymosi, J.. Roth-type theorems in finite groups. J. European Combin. 34 (2013), 1454–1458.CrossRefGoogle Scholar
Tao, T.. 254B, Notes 1: equidistribution of polynomial sequences in tori https://terrytao.wordpress.com/2010/03/28/254b-notes-1-equidistribution-of-polynomial-sequences-in-torii/. Also see Tao, T., Higher order fourier analysis. vol. 142 American Mathematical Soc. (2012).Google Scholar
Tao, T.. Open question: triangle and diamond densities in large dense graphs. https://terrytao.wordpress.com/2007/04/01/open-question-triangle-and-diamond-densities-in-large-dense-graphs/.Google Scholar
Zhao, Y.. Hypergraph limits: a regularity approach. Random Structures Algorithms 47 (2015), 205–226.CrossRefGoogle Scholar