Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T03:02:16.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Torelli theorem for the moduli space of framed bundles

Published online by Cambridge University Press:  26 November 2009

I. BISWAS ,
T. GÓMEZ  and
V. MUÑOZ
I. BISWAS
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005, India. e-mail: [email protected]
T. GÓMEZ
Affiliation:
Instituto de Ciencias Matemáticas CSIC-UAM-UC3M-UCM, Serrano 113bis, 28006 Madrid, Spain and Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, Spain. e-mail: [email protected], [email protected]
V. MUÑOZ
Affiliation:
Instituto de Ciencias Matemáticas CSIC-UAM-UC3M-UCM, Serrano 113bis, 28006 Madrid, Spain and Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, Spain. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be an irreducible smooth complex projective curve of genus g ≥ 2, and let x ∈ X be a fixed point. Fix r > 1, and assume that g > 2 if r = 2. A framed bundle is a pair (E, φ), where E is coherent sheaf on X of rank r and fixed determinant ξ, and φ: Ex → r is a non–zero homomorphism. There is a notion of (semi)stability for framed bundles depending on a parameter τ > 0, which gives rise to the moduli space of τ–semistable framed bundles 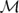τ. We prove a Torelli theorem for 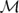τ, for τ > 0 small enough, meaning, the isomorphism class of the one–pointed curve (X, x), and also the integer r, are uniquely determined by the isomorphism class of the variety 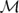τ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 3 , May 2010 , pp. 409 - 423
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F.Vector bundles over an elliptic curve. Proc. London Math. Soc. (3) 7 (1957), 414–452.CrossRefGoogle Scholar
[2]Atiyah, M. F. and Bott, R.The Yang-Mills equations over Riemann surfaces. Roy. Soc. London Philos. Trans. Ser. A 308 (1982), 523–615.Google Scholar
[3]Biswas, I., Brambila-Paz, L. and Newstead, P. E.Stability of projective Poincaré and Picard bundles. Bull. Lond. Math. Soc. 41 (2009), no. 3, 458–472.CrossRefGoogle Scholar
[4]Biswas, I. and Gómez, T.Simplicity of stable principal sheaves. Bull. Lond. Math. Soc. 40 (2008), 163–171.CrossRefGoogle Scholar
[5]Bradlow, S. B., García-Prada, O., Mercat, V., Muñoz, V. and Newstead, P. E.On the geometry of moduli spaces of coherent systems on algebraic curves. Internat. J. Math. 18 (2007), 411–453.CrossRefGoogle Scholar
[6]Brambila-Paz, L., Grzegorczyk, I. and Newstead, P. E.Geography of Brill-Noether loci for small slopes. J. Alg. Geom. 6 (1997), 645–669.Google Scholar
[7]Drézet, J.-M. and Narasimhan, M. S.Groupe de Picard des variétés de modules de fibrés semi-stables sur les courbes algébriques. Invent. Math. 97 (1989), 53–94.CrossRefGoogle Scholar
[8]Hitchin, N.Stable bundles and integrable systems. Duke Math. J. 54 (1987), 91–114.CrossRefGoogle Scholar
[9]Huybrechts, D. and Lehn, M.Framed modules and their moduli. Internat. J. Math. 6 (1995), 297–324.CrossRefGoogle Scholar
[10]Huybrechts, D. and Lehn, M. The geometry of moduli spaces of sheaves. Aspects of Mathematics E31, (Vieweg, Braunschweig/Wiesbaden 1997).CrossRefGoogle Scholar
[11]Kouvidakis, A. and Pantev, T.The automorphism group of the moduli space of semistable vector bundles. Math. Ann. 302 (1995), 225–268.CrossRefGoogle Scholar
[12]Luna, D. Slices étales. Sur les groupes algébriques. pp. 81–105. Bull. Soc. Math. France, Paris, Memoire 33 Soc. Math. France, Paris, 1973.CrossRefGoogle Scholar
[13]Maruyama, M.Openness of a family of torsion free sheaves. Jour. Math. Kyoto Univ. 16 (1976), 627–637.Google Scholar
[14]Narasimhan, M. S. and Ramanan, S. Geometry of Hecke cycles I, C. P. Ramanujam – a tribute. pp. 291–345. Tata Inst. Fund. Res. Studies in Math., 8 (Springer, 1978).Google Scholar
[15]Seshadri, C. S.Fibrés vectoriels sur les courbes algébriques. Astérisque 96 (1982), 209 pp.Google Scholar
[16]Simpson, C.Moduli of representations of the fundamental group of a smooth projective variety I. Publ. Math. IHES 79 (1994), 47–129.CrossRefGoogle Scholar
[17]Tyurin, A. N.Classification of vector bundles over an algebraic curve of arbitrary genus. Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965), 657–688.Google Scholar