Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T01:53:05.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric Auslander and Bass categories

Published online by Cambridge University Press:  18 January 2011

PETER JØRGENSEN  and
KIRIKO KATO
PETER JØRGENSEN
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU. e-mail: [email protected], url: http://www.staff.ncl.ac.uk/peter.jorgensen
KIRIKO KATO
Affiliation:
Department of Mathematics and Information Sciences, Osaka Prefecture University, Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define the symmetric Auslander category As(R) to consist of complexes of projective modules whose left- and right-tails are equal to the left- and right-tails of totally acyclic complexes of projective modules.

The symmetric Auslander category contains A(R), the ordinary Auslander category. It is well known that A(R) is intimately related to Gorenstein projective modules, and our main result is that As(R) is similarly related to what can reasonably be called Gorenstein projective homomorphisms. Namely, there is an equivalence of triangulated categories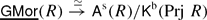where GMor(R) is the stable category of Gorenstein projective objects in the abelian category Mor(R) of homomorphisms of R-modules.

This result is set in the wider context of a theory for As(R) and Bs(R), the symmetric Bass category which is defined dually.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 150 , Issue 2 , March 2011 , pp. 227 - 240
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Auslander, M. Representation dimension of Artin algebras. Queen Mary College Mathematics Notes (Queen Mary College, London, 1971). Reprinted pp. 505–574 in Selected works of Maurice Auslander vol. 1 (edited by Smalø, Reiten, and Solberg, ). Amer. Math. Soc. (Providence, 1999).Google Scholar
[2]Avramov, L. L. and Foxby, H.-B.Ring homomorphisms and finite Gorenstein dimension. Proc. London Math. Soc. (3) 75 (1997), 241–270.CrossRefGoogle Scholar
[3]Christensen, L. W.Frankild, A. and Holm, H.On Gorenstein projective, injective and flat dimensions – A functorial description with applications. J. Algebra 302 (2006), 231–279.Google Scholar
[4]Enochs, E. E. and Jenda, O. M. G.Gorenstein injective and projective modules. Math. Z. 220 (1995), 611–633.CrossRefGoogle Scholar
[5]Hartshorne, R.Residues and duality. With an appendix by P. Deligne. Lecture Notes in Math. break vol. 20 (Springer, 1966).Google Scholar
[6]Iyama, O.Kato, K. and Miyachi, J.-I. Recollement of homotopy categories and Cohen-Macaulay modules, preprint, 2009. math.RA/0911.0172.Google Scholar
[7]Iyengar, S. and Krause, H.Acyclicity versus total acyclicity for complexes over noetherian rings. Doc. Math. 11 (2006), 207–240.Google Scholar
[8]Neeman, A. Triangulated categories. Ann. of Math. Stud. vol. 148 (Princeton University Press, 2001).Google Scholar
[9]Spaltenstein, N.Resolutions of unbounded complexes. Compositio Math. 65 (1988), 121–154.Google Scholar