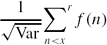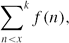Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chatterjee, Sourav
and
Soundararajan, Kannan
2012.
Random Multiplicative Functions in Short Intervals.
International Mathematics Research Notices,
Vol. 2012,
Issue. 3,
p.
479.
Harper, Adam J.
2013.
Bounds on the suprema of Gaussian processes, and omega results for the sum of a random multiplicative function.
The Annals of Applied Probability,
Vol. 23,
Issue. 2,
Harper, Adam J.
Nikeghbali, Ashkan
and
Radziwiłł, Maksym
2015.
Analytic Number Theory.
p.
145.
Aymone, M.
and
Sidoravicius, V.
2017.
Partial sums of biased random multiplicative functions.
Journal of Number Theory,
Vol. 172,
Issue. ,
p.
343.
Mahatab, Kamalakshya
2020.
Sixth norm of a Steinhaus chaos.
International Journal of Number Theory,
Vol. 16,
Issue. 06,
p.
1295.
HARPER, ADAM J.
2020.
MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS.
Forum of Mathematics, Pi,
Vol. 8,
Issue. ,
AGGARWAL, DAKSH
SUBEDI, UNIQUE
VERREAULT, WILLIAM
ZAMAN, ASIF
and
ZHENG, CHENGHUI
2022.
Sums of random multiplicative functions over function fields with few irreducible factors.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 173,
Issue. 3,
p.
715.
Klurman, Oleksiy
Shkredov, Ilya D.
and
Xu, Max Wenqiang
2023.
On the random Chowla conjecture.
Geometric and Functional Analysis,
Vol. 33,
Issue. 3,
p.
749.
Soundararajan, Kannan
and
Xu, Max Wenqiang
2023.
Central limit theorems for random multiplicative functions.
Journal d'Analyse Mathématique,
Vol. 151,
Issue. 1,
p.
343.
Xu, Max Wenqiang
2024.
Better than square-root cancellation for random multiplicative functions.
Transactions of the American Mathematical Society, Series B,
Vol. 11,
Issue. 14,
p.
482.
Wang, Victor Y.
and
Xu, Max Wenqiang
2024.
Paucity phenomena for polynomial products.
Bulletin of the London Mathematical Society,
Vol. 56,
Issue. 8,
p.
2718.
Aymone, Marco
2024.
Sign changes of the partial sums of a random multiplicative function II.
Comptes Rendus. Mathématique,
Vol. 362,
Issue. G8,
p.
895.