Spinors in Hilbert space
Published online by Cambridge University Press: 24 October 2008
Extract
In 1913, É. Cartan discovered that the special orthogonal group SO(k) has a ‘two-valued’ representation (i.e. a projective representation) on a complex vector space S of dimension 2n, where k = 2n or 2n + 1. The projective representation in question lifts to a true representation of the double cover Spin (k) of SO(k). We restrict attention to the case k = 2n. Under the action of Spin (2n), S breaks up into 2 irreducible subspaces:
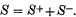
The vectors in S are called spinors (relative to SO(2n)), those in S+ or S− are called half-spinors (4).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 2 , September 1976 , pp. 337 - 347
- Copyright
- Copyright © Cambridge Philosophical Society 1976
References
REFERENCES
- 4
- Cited by


