Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T01:16:10.207Z Has data issue: false hasContentIssue false
  • English
  • Français

The spectrum of the Cesàro operator on c0(c0)

Published online by Cambridge University Press:  24 October 2008

J. Okutoyi  and
B. Thorpe
J. Okutoyi
Affiliation:
Department of Mathematics, Kenyatta University College, Nairobi, Kenya
B. Thorpe
Affiliation:
Department of Mathematics, University of Birmingham, Birmingham B15 2TT
Get access Rights & Permissions [Opens in a new window]

Extract

1. In a recent paper [6], the spectrum of the Cesàro operator C on c0 (the space of null sequences of complex numbers with the sup norm) was obtained by finding the eigenvalues of the adjoint operator on 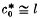and showing that the operator (C–λI)−1 lies in B(c0) for all λ outside the closure of this set of eigenvalues. In this paper we apply a similar method to find the spectrum of the two-dimensional Cesàro operator on a space of double sequences c0(c0) (defined in §2). We shall introduce a simplification to the proof in [6] by observing that (C – λI)−1, when it exists, is a Hausdorff summability method (see page 288 of [11] for the single variable case on the space of convergent sequences c), and the crux of our proof is to show that the moment constant associated with the method (C – λI)−1 is regular for the space c0(c0) and the set of λ under consideration. It turns out that c0(c0) ≅ c0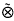c0 (see page 237 of [7]) and that the two-dimensional Cesàro operator on c0(c0) is the tensor product C ⊗ C of the Cesàro operator C on c0. Thus our result gives a direct proof that the spectrum σ(C ⊗ C) equals σ(C)σ(C), which is a special case of the result of Schechter in [8].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 123 - 129
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, C. R.. Hausdorff transformations for double sequences. Bull. Amer. Math. Soc. 39 (1933), 303–312.CrossRefGoogle Scholar
[2]Jakimovski, A. and Russell, D. C.. Representation of continuous linear functionals on a subspace of a countable cartesian product of Banach spaces. Studia Math. 72 (1982), 273–284.CrossRefGoogle Scholar
[3]Maddox, I. J.. Infinite Matrices of Operators. Lecture Notes in Math. vol. 786 (Springer-Verlag, 1980).CrossRefGoogle Scholar
[4]McShane, E. J.. Unified Integration (Academic Press, 1983).Google Scholar
[5]Ramanujan, M. S.. On Hausdorff transformations for double sequences. Proc. Indian Acad. Sci. A 42 (1955), 131–135.CrossRefGoogle Scholar
[6]Reade, J. B.. On the spectrum of the Cesàro operator. Bull. London Math. Soc. 17 (1985), 263–267.CrossRefGoogle Scholar
[7]Schaefer, H. H.. Banach Lattices and Positive Operators (Springer-Verlag, 1974).CrossRefGoogle Scholar
[8]Schechter, M.. On the spectra of operators on tensor products. J. Funct. Anal. 4 (1969), 95–99.CrossRefGoogle Scholar
[9]Ustina, F.. The Hausdorff means for double sequences. Canad. Math. Bull. 10 (1967), 347–352.CrossRefGoogle Scholar
[10]Watson, G. N.. A Treatise on the Theory of Bessel Functions (Cambridge University Press, 1944).Google Scholar
[11]Wilansky, A.. Summability through Functional Analysis (North-Holland, 1984).Google Scholar