Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bressoud, D. M.
1981.
Analytic Number Theory.
Vol. 899,
Issue. ,
p.
325.
Gessel, Ira
and
Stanton, Dennis
1983.
Applications of 𝑞-Lagrange inversion to basic hypergeometric series.
Transactions of the American Mathematical Society,
Vol. 277,
Issue. 1,
p.
173.
Bressoud, D. M.
1983.
A matrix inverse.
Proceedings of the American Mathematical Society,
Vol. 88,
Issue. 3,
p.
446.
Andrews, G. E.
1983.
Truncation of the Rogers–Ramanujan Theta Series.
SIAM Review,
Vol. 25,
Issue. 3,
p.
402.
Jordan, W. B.
1984.
Truncation of the Rogers–Ramanujan Theta Series (G. E. Andrews).
SIAM Review,
Vol. 26,
Issue. 3,
p.
433.
Andrews, George E.
1989.
q-Series and Partitions.
Vol. 18,
Issue. ,
p.
1.
Krattenthaler, C.
1996.
A new matrix inverse.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 1,
p.
47.
Milne, Stephen C.
1997.
Balanced3ϕ2Summation Theorems forU(n) Basic Hypergeometric Series.
Advances in Mathematics,
Vol. 131,
Issue. 1,
p.
93.
Andrews, George E.
2001.
Special Functions 2000: Current Perspective and Future Directions.
p.
1.
Warnaar, S. Ole
2001.
Algebraic Combinatorics and Applications.
p.
333.
Agarwal, A. K.
and
Padmavathamma
2002.
Number Theory and Discrete Mathematics.
p.
53.
Agarwal, A. K.
and
Padmavathamma
2002.
Number Theory and Discrete Mathematics.
p.
53.
Huang, I-Chiau
2002.
Inverse Relations and Schauder Bases.
Journal of Combinatorial Theory, Series A,
Vol. 97,
Issue. 2,
p.
203.
Warnaar, S.Ole
2003.
The generalized Borwein conjecture. II. Refined q-trinomial coefficients.
Discrete Mathematics,
Vol. 272,
Issue. 2-3,
p.
215.
Sills, Andrew V.
2004.
RRtools—a Maple package for aiding the discovery and proof of finite Rogers–Ramanujan type identities.
Journal of Symbolic Computation,
Vol. 37,
Issue. 4,
p.
415.
Andrews, George E.
2005.
Theory and Applications of Special Functions.
Vol. 13,
Issue. ,
p.
39.
Andrews, George E.
and
Warnaar, S. Ole
2007.
The Bailey transform and false theta functions.
The Ramanujan Journal,
Vol. 14,
Issue. 1,
p.
173.
Ma, Xinrong
2007.
The (f,g)-inversion formula and its applications: The (f,g)-summation formula.
Advances in Applied Mathematics,
Vol. 38,
Issue. 2,
p.
227.
Chan, Hei-Chi
2007.
From Andrews’ formula for the Fibonacci numbers to the Rogers-Ramanujan identities.
The Fibonacci Quarterly,
Vol. 45,
Issue. 3,
p.
221.
Mc Laughlin, James
and
Zimmer, Peter
2008.
Some identities between basic hypergeometric series deriving from a new Bailey-type transformation.
Journal of Mathematical Analysis and Applications,
Vol. 345,
Issue. 2,
p.
670.


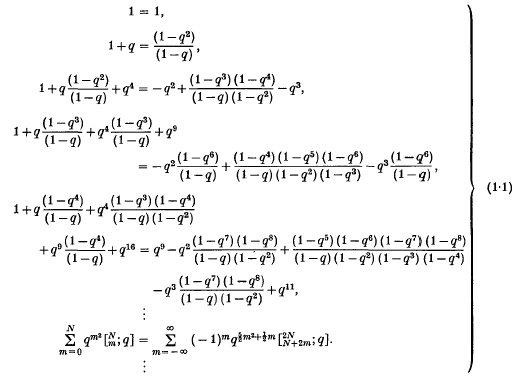
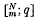 is the Gaussian polynomial denned to be zero for
is the Gaussian polynomial denned to be zero for