Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T17:20:16.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Some generalizations of two-point expansions

Published online by Cambridge University Press:  24 October 2008

Sheila Scott Macintyre
Sheila Scott Macintyre
Affiliation:
The UniversityAberdeen
Get access Rights & Permissions [Opens in a new window]

Extract

Abel's series(1)

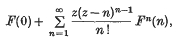
may be regarded as a generalization of the Taylor expansion

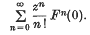
This note generalizes the two-point series of Lidstone and Whittaker (see (9)) in a similar way. Alternatively, the series discussed might be regarded as generalizations of Abel's series.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 4 , October 1952 , pp. 583 - 586
Copyright
Copyright © Cambridge Philosophical Society 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Abel, N. H.Oeuvres complètes (Christiania, 1839).Google Scholar
(2)Buck, R. C.Interpolation series. Trans. Amer. math. Soc. 64 (1948), 283–98.CrossRefGoogle Scholar
(3)Gontcharoff, W.Sur un procédé d'itération. Commun. Soc. math. Kharkoff (4), 5 (1932), 67–85.Google Scholar
(4)MacIntyre, A. J.Laplace's transformation and integral functions. Proc. Lond. math. Soc. (2), 45 (1939), 1–20.CrossRefGoogle Scholar
(5)MacIntyre, A. J. and MacIntyre, , Sheila, Scott. Theorems on the convergence and asymptotic validity of Abel's series. Proc. roy. Soc. Edinb. 63 (1952), 222–31.Google Scholar
(6)Polya, G. and Szego, G.Aufgaben und Lehrsätze, vol. 1 (New York, 1945).Google Scholar
(7)Poritsky, H.On certain polynomial and other approximations to analytic functions. Trans. Amer. math. Soc. 34 (1932), 274–331.CrossRefGoogle Scholar
(8)Schmidli, S. Über gewisse Interpolationsreihen (Thesis, Zürich, 1942).Google Scholar
(9)Whittaker, J. M.On Lidstone's series and two-point expansions of analytic functions. Proc. Lond. math. Soc. (2), 36 (1933–1994), 451–69.Google Scholar