Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T02:13:26.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Some further results in infinite divisibility

Published online by Cambridge University Press:  24 October 2008

D. N. Shanbhag ,
D. Pestana  and
M. Sreehari
D. N. Shanbhag
Affiliation:
University of Sheffield and University of Baroda
D. Pestana
Affiliation:
University of Sheffield and University of Baroda
M. Sreehari
Affiliation:
University of Sheffield and University of Baroda
Get access Rights & Permissions [Opens in a new window]

Extract

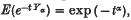Goldie (2), Steutel (8, 9), Kelker (4), Keilson and Steutel (3) and several others have studied the mixtures of certain distributions which are infinitely divisible. Recently Shanbhag and Sreehari (7) have proved that if Z is exponential with unit parameter and for 0 < α < 1, if Yx is a positive stable random variable with , t ≥ 0 and independent of Z, then for every 0 < α < 1

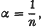Using this result, they have obtained several interesting results concerning stable random variables including some extensions of the results of the above authors. More recently, Williams (11) has used the same approach to show that if , where n is a positive integer ≥ 2, then 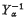is distributed as the product of n − 1 independent gamma random variables with index parameters α, 2α, …, (n − 1) α. Prior to these investigations, Zolotarev (12) had studied the problems of M-divisibility of stable laws.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 2 , September 1977 , pp. 289 - 295
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Higher transcendental functions, vol. I (New York, Toronto, London: McGraw-Hill Book Company, 1953).Google Scholar
(2)Goldie, C. M.A class of infinitely divisible distributions. Proc. Cambridge Philos. Soc. 63 (1967), 1141–1143.CrossRefGoogle Scholar
(3)Keilbon, J. and Steutel, F. W.Mixtures of distributions, moment inequalities and measures of exponentiality and normality. Ann. Probability 2 (1974), 112–130.Google Scholar
(4)Kelker, D.Infinite divisibility and variance mixtures of the normal distribution. Ann. Math. Statist. 42 (1971), 802–808.CrossRefGoogle Scholar
(5)Lukacs, E.Characteristic functions, 2nd edn (London: Griffin, 1970).Google Scholar
(6)Ruegg, A. F.A characterization of certain infinitely divisible laws. Ann. Math. Statist. 41 (1970), 1354–1356.CrossRefGoogle Scholar
(7)Shanbhag, D. N. and Sreehari, M.On certain self-decomposable distributions. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 38 (1977), 217–222.CrossRefGoogle Scholar
(8)Steutel, F. W.Preservation of infinite divisibility under mixing and related topics. Math. Centre Tracts 33, Math. Centre (Amsterdam, 1970).Google Scholar
(9)Steutel, F. W.Some recent results in infinite divisibility. Stoch. Processes Appl. 1 (1973), 125–143.CrossRefGoogle Scholar
(10)Whittaker, E. T. and Watson, G. N.A course of modern analysis, 4th edn (Cambridge University Press, 1963).Google Scholar
(11)Williams, E. J.Some representations of stable random variables as products. Biometrika 64 (1977), 167–169.CrossRefGoogle Scholar
(12)Zolotarev, V. M.On the divisibility of stable laws. Theor. Probability Appl. 12 (1967), 506–508.CrossRefGoogle Scholar