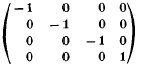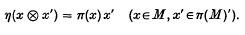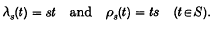Research Article
A generalization of the Königsberg bridges problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
Applications of outwardly simple line families to plane convex sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 353-356
-
- Article
- Export citation
The eighty-one types of isohedral tilings in the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-196
-
- Article
- Export citation
On the coefficients of certain automorphic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-367
-
- Article
- Export citation
The non-existence of a certain finite projective plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-12
-
- Article
- Export citation
A commutative Noetherian ring which possesses a dualizing complex is acceptable
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 197-213
-
- Article
- Export citation
A dual approach to Černikov modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 215-239
-
- Article
- Export citation
On the Banach–Saks property
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-374
-
- Article
- Export citation
On the crystallography of infinite Coxeter groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-24
-
- Article
- Export citation
Primitive irreducible representations of nilpotent groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 241-247
-
- Article
- Export citation
On non-unital Jordan–Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-380
-
- Article
- Export citation
The associated graded ring of an integral group ring
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-33
-
- Article
- Export citation
Some unexpectedly non-singular orbit spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-37
-
- Article
- Export citation
The 2-primary J-homomorphism
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-387
-
- Article
- Export citation
Exact sequences of conjugacy classes and rationalization
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-253
-
- Article
- Export citation
On stratifying 3-jets of functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-400
-
- Article
- Export citation
Injective W*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 39-47
-
- Article
- Export citation
The positive-definiteness of the complete symmetric functions of even order
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-258
-
- Article
- Export citation
Spectra of derivations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-57
-
- Article
- Export citation
The ideal structure of the Stone-Čech compactification of a group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-409
-
- Article
- Export citation

 = {
= {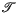 is called
is called 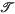 . Clearly every monohedral tiling is locally finite.
. Clearly every monohedral tiling is locally finite.

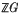 . Suppose that
. Suppose that 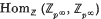 of a quasi-cyclic
of a quasi-cyclic 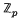 of
of 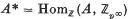 is a free
is a free 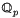 of
of 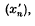 ), which is (
), which is (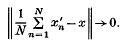
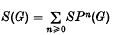 the symmetric algebra of
the symmetric algebra of 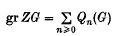 the associated graded ring of the integral group ring
the associated graded ring of the integral group ring 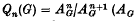 (
(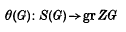
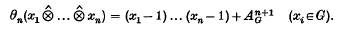
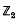 given by the matrix.
given by the matrix.