Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T03:21:57.470Z Has data issue: false hasContentIssue false
  • English
  • Français

Schauder bases and decompositions in locally convex spaces

Published online by Cambridge University Press:  24 October 2008

J. H. Webb
J. H. Webb
Affiliation:
University of Cape Town, Rondesbosch C.P., South Africa
Get access Rights & Permissions [Opens in a new window]

Extract

Let E[τ] be a locally convex Hausdorif topological vector space, with a Schauder basis {xi, x′j where

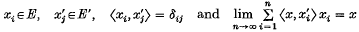
for each x ∈ E. The partial summation operator Sn, defined by

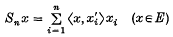
is a linear operator on E, whose definition extends at once to a linear operator mapping (E′)* into E, where (E′)* is the algebraic dual of E′. The dual of Sn is the operator S′n, mapping E* into E′, defined by

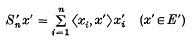
and 〈Snx, x′〉 = 〈x, S′nx′〉 for each x ∈ (E′)*. It is easy to see that S′nx′ → x′ with respect to the weak topology σ(E′, E) for each x′ ∈ E′.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 76 , Issue 1 , July 1974 , pp. 145 - 152
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Arsove, M. G. and Edwards, R. E.Generalized bases in topological linear spaces. Studia Math. 19 (1960), 95–113.CrossRefGoogle Scholar
(2)CooK, T. A.Schauder decompositions and semi-reflexive spaces. Math. Ann. 182 (1969), 232–235.CrossRefGoogle Scholar
(3)De Wilde, M. and Houet, C.On increasing sequences of absolutely convex sets in locally convex spaces. Math. Ann. 192 (1971), 257–261.CrossRefGoogle Scholar
(4)Hampson, J. K. and Wilansky, A.Sequences in locally convex spaces. Studia Math. 65 (1973), 221–223.CrossRefGoogle Scholar
(5)James, R. C.Bases and reflexivity of Banach spaces. Ann. of Math. 52 (1950), 518–527.CrossRefGoogle Scholar
(6)Kalton, N. J.Schauder decompositions and completeness. Bull. London Math. Soc. 2 (1970), 34–36.CrossRefGoogle Scholar
(7)Kalton, N.3. Schauder decompositions in locally convex spaces. Proc. Cambridge Philos. Soc. 68 (1970), 377–392.CrossRefGoogle Scholar
(8)Kalton, N.3. Mackey duals and almost shrinking bases. Proc. Cambridge Philos. Soc. 74 (1973), 73–81.CrossRefGoogle Scholar
(9)Köthe, G.Topological vector spaces. I (Springer, 1969).Google Scholar
(10)Webb, J. H.Sequential convergence in locally convex spaces. Proc. Cambridge Philos. Soc. 64 (1968), 341–364.CrossRefGoogle Scholar