Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T01:40:32.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Relation between Mean Stopping Power and Mean Range of β-rays.

Published online by Cambridge University Press:  24 October 2008

E. J. Williams
E. J. Williams
Affiliation:
1851 Exhibition Senior Research Student, Gonville and Caius College
Get access Rights & Permissions [Opens in a new window]

Extract

Wilson's cloud method, provides a means of measuring the ranges of β-rays which is free from any uncertainties arising from the scattering of the rays, and for this reason it is an invaluable method for obtaining the true rate of loss of energy of β-rays as they traverse matter. Thetrue rate of loss of energy or ‘stopping power’ is defined as the quantity 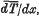, where 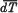is the mean energy lost by β-rays of energy T in travelling a distance dx measured along their paths. The cloud method of course enables one to observe only the total ranges of β-particles, and in deducing the stopping power from the mean range it is necessary to bear in mind that owing to ‘straggling,’ which in the case of β-rays is large, the differential coefficient 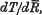, where 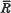is the mean range of particles of energy T, is not exactly the same as the stopping power 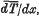. 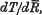is however the quantity which the cloud method enables us to observe. It is the purpose of this note to consider the exact relation between these two quantities so that the information provided by the cloud method may be rigorously interpreted.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 24 , Issue 2 , April 1928 , pp. 315 - 319
Copyright
Copyright © Cambridge Philosophical Society 1928

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* This can be done without increasing the probability of ‘double’ collisions. For if n be the total number of particles the average number which suffer single collisions, in which the energy lost lies between Q and Q + dQ, is ø (Q) dQdx × n and is proportional to ndx. The number which suffer double collisions is

and is proportional to n (dx)2. It follows that by choosing dx sufficiently small the former may be made as large as we please without affecting the latter.

* If, in observing R, ‘tracks’ with ‘branches’ greater than a certain length are omitted then the effective value of M is less than T and the correction is correspondingly less.