Research Article
The average value of an exponential function over the lattice points of a circle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 171-179
-
- Article
- Export citation
Limiting forms of the frequency distribution of the largest or smallest member of a sample
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 180-190
-
- Article
- Export citation
On the quintic surface in space of five dimensions. (Part II, Curves on the surface.*)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 191-209
-
- Article
- Export citation
An Involution in the Complex Variable
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-217
-
- Article
- Export citation
Extension of a Lemma of Stroh
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 218-222
-
- Article
- Export citation
The Second Solution of Mathieu's Differential Equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-230
-
- Article
- Export citation
Operational Solution of Some Problems in Viscous Fluid Motion
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-235
-
- Article
- Export citation
A recording gyroscope
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 236-250
-
- Article
- Export citation
On the Action of the Geiger α-particle Counter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-258
-
- Article
- Export citation
The High-frequency Electric Discharge at Low Pressures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-267
-
- Article
- Export citation
On the Formation of a Gaseous Helide of Radium Active Deposit
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 268-275
-
- Article
- Export citation
A dynamical method for the determination of Young's modulus by stretching
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 276-279
-
- Article
- Export citation
An Asymptotic Expansion for
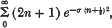
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 280-289
-
- Article
- Export citation
The Specific Heat of Carbon Dioxide—Correction
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 290
-
- Article
- Export citation
On the present position of the Theory of Centres of Activity in Heterogeneous Catalysis
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-306
-
- Article
- Export citation
A Method of Generalising the Law of Mass Action for Heterogeneous Surface Reactions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-314
-
- Article
- Export citation
Relation between Mean Stopping Power and Mean Range of β-rays.
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-319
-
- Article
- Export citation
The Photo-Electric Threshold and the Heat of Dissociation of the Potassium Molecule
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 320-327
-
- Article
- Export citation
A Theory of Hartree's Atomic Fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 328-342
-
- Article
- Export citation
Some Applications and Implications of Duane's Quantum Theory of Diffraction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-356
-
- Article
- Export citation

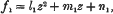
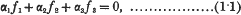
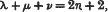
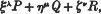
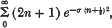
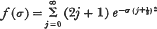
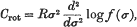
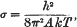
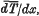 , where
, where 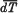 is the mean energy lost by β-rays of energy
is the mean energy lost by β-rays of energy 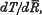 , where
, where 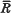 is the mean range of particles of energy
is the mean range of particles of energy